101133: [AtCoder]ABC113 D - Number of Amidakuji

Problem Statement

Amidakuji is a traditional method of lottery in Japan.

To make an amidakuji, we first draw $W$ parallel vertical lines, and then draw horizontal lines that connect them. The length of each vertical line is $H+1$ [cm], and the endpoints of the horizontal lines must be at $1, 2, 3, ...,$ or $H$ [cm] from the top of a vertical line.

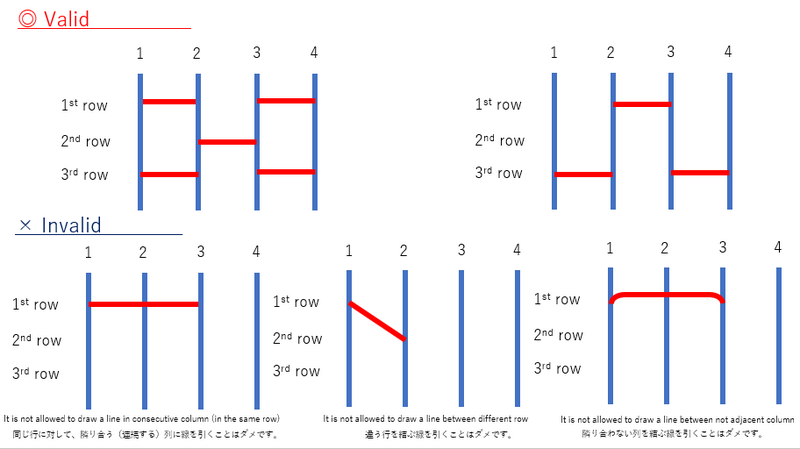
A valid amidakuji is an amidakuji that satisfies the following conditions:

• No two horizontal lines share an endpoint.
• The two endpoints of each horizontal lines must be at the same height.
• A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition, modulo $1\ 000\ 000\ 007$: if we trace the path from the top of the leftmost vertical line to the bottom, always following horizontal lines when we encounter them, we reach the bottom of the $K$-th vertical line from the left.

For example, in the following amidakuji, we will reach the bottom of the fourth vertical line from the left.

Constraints

• $H$ is an integer between $1$ and $100$ (inclusive).
• $W$ is an integer between $1$ and $8$ (inclusive).
• $K$ is an integer between $1$ and $W$ (inclusive).

Input

Input is given from Standard Input in the following format:

$H$ $W$ $K$

Output

Print the number of the amidakuji that satisfy the condition, modulo $1\ 000\ 000\ 007$.

Sample Input 1

1 3 2

Sample Output 1

1

Only the following one amidakuji satisfies the condition:

Sample Input 2

1 3 1

Sample Output 2

2

Only the following two amidakuji satisfy the condition:

Sample Input 3

2 3 3

Sample Output 3

1

Only the following one amidakuji satisfies the condition:

Sample Input 4

2 3 1

Sample Output 4

5

Only the following five amidakuji satisfy the condition:

Sample Input 5

7 1 1

Sample Output 5

1

As there is only one vertical line, we cannot draw any horizontal lines. Thus, there is only one amidakuji that satisfies the condition: the amidakuji with no horizontal lines.

Sample Input 6

15 8 5

Sample Output 6

437760187

Be sure to print the answer modulo $1\ 000\ 000\ 007$.