200592: [AtCoder]ARC059 E - Children and Candies

Problem Statement

12:17 (UTC): The sample input 1 and 2 were swapped. The error is now fixed. We are very sorry for your inconvenience.

There are $N$ children in AtCoder Kindergarten, conveniently numbered $1$ through $N$. Mr. Evi will distribute $C$ indistinguishable candies to the children.

If child $i$ is given $a$ candies, the child's happiness will become $x_i^a$, where $x_i$ is the child's excitement level. The activity level of the kindergarten is the product of the happiness of all the $N$ children.

For each possible way to distribute $C$ candies to the children by giving zero or more candies to each child, calculate the activity level of the kindergarten. Then, calculate the sum over all possible way to distribute $C$ candies. This sum can be seen as a function of the children's excitement levels $x_1,..,x_N$, thus we call it $f(x_1,..,x_N)$.

You are given integers $A_i,B_i (1≦i≦N)$. Find 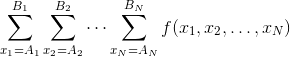modulo $10^9+7$.

Constraints

• $1≦N≦400$
• $1≦C≦400$
• $1≦A_i≦B_i≦400 (1≦i≦N)$

Partial Score

• $400$ points will be awarded for passing the test set satisfying $A_i=B_i (1≦i≦N)$.

Input

The input is given from Standard Input in the following format:

$N$ $C$
$A_1$ $A_2$ ... $A_N$
$B_1$ $B_2$ ... $B_N$

Output

Print the value of 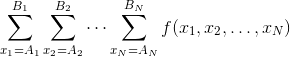modulo $10^9+7$.

Sample Input 1

2 3
1 1
1 1

Sample Output 1

4

This case is included in the test set for the partial score, since $A_i=B_i$. We only have to consider the sum of the activity level of the kindergarten where the excitement level of both child $1$ and child $2$ are $1$ ($f(1,1)$).

• If child $1$ is given $0$ candy, and child $2$ is given $3$ candies, the activity level of the kindergarten is $1^0*1^3=1$.
• If child $1$ is given $1$ candy, and child $2$ is given $2$ candies, the activity level of the kindergarten is $1^1*1^2=1$.
• If child $1$ is given $2$ candies, and child $2$ is given $1$ candy, the activity level of the kindergarten is $1^2*1^1=1$.
• If child $1$ is given $3$ candies, and child $2$ is given $0$ candy, the activity level of the kindergarten is $1^3*1^0=1$.

Thus, $f(1,1)=1+1+1+1=4$, and the sum over all $f$ is also $4$.

Sample Input 2

1 2
1
3

Sample Output 2

14

Since there is only one child, child $1$'s happiness itself will be the activity level of the kindergarten. Since the only possible way to distribute $2$ candies is to give both candies to child $1$, the activity level in this case will become the value of $f$.

• When the excitement level of child $1$ is $1$, $f(1)=1^2=1$.
• When the excitement level of child $1$ is $2$, $f(2)=2^2=4$.
• When the excitement level of child $1$ is $3$, $f(3)=3^2=9$.

Thus, the answer is $1+4+9=14$.

Sample Input 3

2 3
1 1
2 2

Sample Output 3

66

Since it can be seen that $f(1,1)=4 , f(1,2)=15 , f(2,1)=15 , f(2,2)=32$, the answer is $4+15+15+32=66$.

Sample Input 4

4 8
3 1 4 1
3 1 4 1

Sample Output 4

421749

This case is included in the test set for the partial score.

Sample Input 5

3 100
7 6 5
9 9 9

Sample Output 5

139123417