Caterpillar

题意翻译

## 题目描述 一个毛毛虫定义为 一个无向联通无环图上 存在一条路径 $p$ 使得任意一个节点距离 $p$ 的距离至多为 $1$ 。 毛毛虫可以包含自环 （ 一条从一个顶点连向自己的边 ），但是不可以包含重边。 这个图片是一个毛毛虫的例子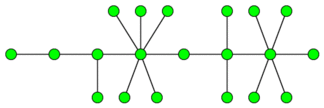：  现在你有一张无向图 $G$ 。你被允许做一些合并操作。 每次操作将两个顶点合并成一个顶点 。 每次选择任意两个顶点 $a ,b (a≠b)$ , 这些顶点以及它们的边 （ 至少连接着 $a,b$ 中一个点的边 ） 将被删除 ，而后顶点 $w$ 会被加入，以及对于每条边 $(x,a),(x,b)$ 都会有新边 $( x,w)$ 加入 。 如果有一条边 $(a,b)$ 它会被转换成自环 $(w,w)$ 。 得到的图 （ 操作结束后 ） 可能会有重边。我们注意到这个操作减少了 $1$ 个顶点 ，却没有改变边的数量。 合并操作可以简单的描述为 将图中两个顶点合并为图中的一个顶点并继承原来所有的边。 你可以连续地使用合并操作，从而将给定的图转变成一个毛毛虫。 编写一个程序，这个程序将要输出这张图转变成一个毛毛虫的最少操作次数。 ## 输入格式 第一行包含两个正整数 $ n,m (1<=n<=20000,1<=m<=10^5)$, $n$ 代表了图中顶点的数量，而 $m$ 则代表了边的数量。 接下来 $m$ 行描述了边的信息 , 每行一条。 每行包含了一对整数 $a_i,b_i(1<=a_i,b_i<=n,a_i≠b_i) $ ，表示 点间的边。 顶点从 $1$ 到 $n$ 编号。 给出的图保证任意两点间不会有多条边。 给出的图不一定联通。 ## 输出格式 输出操作次数的最小值。

题目描述

An undirected graph is called a caterpillar if it is a connected graph without cycles and it has such a path $ p $ that any vertex is located at a distance of at most 1 from the path $ p $ . The caterpillar can contain loops (edges from a vertex to itself) but cannot contain multiple (parallel) edges. The picture contains an example of a caterpillar: You are given an undirected graph $ G $ . You are allowed to do a merging operations, each such operation merges two vertices into one vertex. For that two any vertices $ a $ and $ b $ ( $ a≠b $ ) are chosen. These verteces are deleted together with their edges (which are incident to at least one of the vertices $ a $ or $ b $ ) but a new vertex $ w $ is added together with edges $ (x,w) $ for each edge ( $ a,w $ ) and/or ( $ b,w $ ). If there was the edge $ (a,b) $ it transforms to the loop $ (w,w) $ . The resulting graph (after the merging operation) may contain multiple (parallel) edges between pairs of vertices and loops. Let us note that this operation decreases the number of vertices of graph by 1 but leaves the number of edges in the graph unchanged. The merging operation can be informally described as a unity of two vertices of the graph into one with the natural transformation of the graph edges. You may apply this operation consecutively and make the given graph to be a caterpillar. Write a program that will print the minimal number of merging operations required to make the given graph a caterpillar.

输入输出格式

输入格式

The first line contains a pair of integers $ n $ , $ m $ ( $ 1<=n<=2000;0<=m<=10^{5} $ ), where $ n $ represents the number of vertices in the graph and $ m $ is the number of edges in it. Then the following $ m $ lines contain edge descriptions, one edge description per line. Every line contains a pair of integers $ a_{i},b_{i} $ ( $ 1<=a_{i},b_{i}<=n;a_{i}≠b_{i} $ ), $ a_{i},b_{i} $ which represent the indices of the vertices connected by the edge. The vertices are numbered from 1 to $ n $ . In the given graph it will be no more than one edge between any pair of vertices. The given graph is not necessarily connected.

输出格式

Print the minimal required number of operations.

输入输出样例

输入样例 #1

4 4
1 2
2 3
3 4
4 2

输出样例 #1

2

输入样例 #2

6 3
1 2
3 4
5 6

输出样例 #2

2

输入样例 #3

7 6
1 2
2 3
1 4
4 5
1 6
6 7

输出样例 #3

1

题意翻译

## 题目描述 一个毛毛虫定义为 一个无向联通无环图上 存在一条路径 $p$ 使得任意一个节点距离 $p$ 的距离至多为 $1$ 。 毛毛虫可以包含自环 （ 一条从一个顶点连向自己的边 ），但是不可以包含重边。 这个图片是一个毛毛虫的例子：  现在你有一张无向图 $G$ 。你被允许做一些合并操作。 每次操作将两个顶点合并成一个顶点 。 每次选择任意两个顶点 $a ,b (a≠b)$ , 这些顶点以及它们的边 （ 至少连接着 $a,b$ 中一个点的边 ） 将被删除 ，而后顶点 $w$ 会被加入，以及对于每条边 $(x,a),(x,b)$ 都会有新边 $( x,w)$ 加入 。 如果有一条边 $(a,b)$ 它会被转换成自环 $(w,w)$ 。 得到的图 （ 操作结束后 ） 可能会有重边。我们注意到这个操作减少了 $1$ 个顶点 ，却没有改变边的数量。 合并操作可以简单的描述为 将图中两个顶点合并为图中的一个顶点并继承原来所有的边。 你可以连续地使用合并操作，从而将给定的图转变成一个毛毛虫。 编写一个程序，这个程序将要输出这张图转变成一个毛毛虫的最少操作次数。 ## 输入格式 第一行包含两个正整数 $ n,m (1<=n<=20000,1<=m<=10^5)$, $n$ 代表了图中顶点的数量，而 $m$ 则代表了边的数量。 接下来 $m$ 行描述了边的信息 , 每行一条。 每行包含了一对整数 $a_i,b_i(1<=a_i,b_i<=n,a_i≠b_i) $ ，表示 点间的边。 顶点从 $1$ 到 $n$ 编号。 给出的图保证任意两点间不会有多条边。 给出的图不一定联通。 ## 输出格式 输出操作次数的最小值。