Castle

题意翻译

## 题目描述 Gerald身处一座古老的城堡之中。这座城堡有 $n$ 间大厅与 $n-1$ 个走廊，并且从一间大厅到另一间的道路有且仅有一条，也就是说，由这个城堡所构造的图实际上是一颗树。 一开始，也就是在第0时刻，Gerald处在第1间大厅里。这个城堡中的某个大厅里放着Gerald想要的珍宝。然而Gerald并不知道珍宝的确切位置。珍宝在任何另n-1间大厅的可能性都是相等的。只有身处其中，Gerald才能确定这件大厅中到底有没有珍宝。如果你成功地让Gerald看到他想要的珍宝....除了可以拿到一个绿色的AC以外你也得不到什么好处。 每条走廊都有着不同的长度，所以走过每条走廊的时间不相等。由于这座城堡修建的时候是无良外包商修的，所以走廊走过2次就塌了。也就是说Gerald得找到一种策略，让他确保能够每个大厅都去一遍。 举个栗子：若使Gerald走到第二、第三、第四...间大厅的时间分别为$t_2,t_3,t_4...$，那么Gerald找到珍宝的平均时间就是$\frac{(t_2+t_3+t_4+...+t_n)}{(n-1)}$。 ## 输入及范围: 第一行为大厅的个数 $n,(2\le n\le 10^5) $ 接下来 $n-1$ 行为对各个走廊的描述，包括: 走廊连接的两个大厅 $a_i$ 与 $b_i$ 走过走廊所需要的时间 $t_i$ 再次提醒，Gerald一开始站在1号大厅 ## 输出格式 输出一个实数，即Gerald找到珍宝所需时间的期望值，允许不超过 $10^{-6}$ 的误差

题目描述

Gerald is positioned in an old castle which consists of $ n $ halls connected with $ n-1 $ corridors. It is exactly one way to go from any hall to any other one. Thus, the graph is a tree. Initially, at the moment of time $ 0 $ , Gerald is positioned in hall $ 1 $ . Besides, some other hall of the castle contains the treasure Gerald is looking for. The treasure's position is not known; it can equiprobably be in any of other $ n-1 $ halls. Gerald can only find out where the treasure is when he enters the hall with the treasure. That very moment Gerald sees the treasure and the moment is regarded is the moment of achieving his goal. The corridors have different lengths. At that, the corridors are considered long and the halls are considered small and well lit. Thus, it is possible not to take the time Gerald spends in the halls into consideration. The castle is very old, that's why a corridor collapses at the moment when somebody visits it two times, no matter in which direction. Gerald can move around the castle using the corridors; he will go until he finds the treasure. Naturally, Gerald wants to find it as quickly as possible. In other words, he wants to act in a manner that would make the average time of finding the treasure as small as possible. Each corridor can be used no more than two times. That's why Gerald chooses the strategy in such a way, so he can visit every hall for sure. More formally, if the treasure is located in the second hall, then Gerald will find it the moment he enters the second hall for the first time — let it be moment $ t_{2} $ . If the treasure is in the third hall, then Gerald will find it the moment he enters the third hall for the first time. Let it be the moment of time $ t_{3} $ . And so on. Thus, the average time of finding the treasure will be equal to .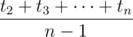

输入输出格式

输入格式

The first line contains the only integer $ n $ ( $ 2<=n<=10^{5} $ ) — the number of halls in the castle. Next $ n-1 $ lines each contain three integers. The $ i $ -th line contains numbers $ a_{i} $ , $ b_{i} $ and $ t_{i} $ ( $ 1<=a_{i},b_{i}<=n $ , $ a_{i}≠b_{i} $ , $ 1<=t_{i}<=1000 $ ) — the numbers of halls connected with the $ i $ -th corridor and the time needed to go along the corridor. Initially Gerald is in the hall number $ 1 $ . It is guaranteed that one can get from any hall to any other one using corridors.

输出格式

Print the only real number: the sought expectation of time needed to find the treasure. The answer should differ from the right one in no less than $ 10^{-6} $ .

输入输出样例

输入样例 #1

2
1 2 1

输出样例 #1

1.0

输入样例 #2

4
1 3 2
4 2 1
3 2 3

输出样例 #2

4.333333333333334

输入样例 #3

5
1 2 1
1 3 1
1 4 1
1 5 1

输出样例 #3

4.0

说明

In the first test the castle only has two halls which means that the treasure is located in the second hall. Gerald will only need one minute to go to the second hall from the first one. In the second test Gerald can only go from the first hall to the third one. He can get from the third room to the first one or to the second one, but he has already visited the first hall and can get nowhere from there. Thus, he needs to go to the second hall. He should go to hall 4 from there, because all other halls have already been visited. If the treasure is located in the third hall, Gerald will find it in a minute, if the treasure is located in the second hall, Gerald finds it in two minutes, if the treasure is in the fourth hall, Gerald will find it in three minutes. The average time makes $ 2 $ minutes. In the third test Gerald needs to visit $ 4 $ halls: the second, third, fourth and fifth ones. All of them are only reachable from the first hall. Thus, he needs to go to those $ 4 $ halls one by one and return. Gerald will enter the first of those halls in a minute, in the second one — in three minutes, in the third one - in $ 5 $ minutes, in the fourth one - in $ 7 $ minutes. The average time is $ 4 $ minutes.

题意翻译

## 题目描述 Gerald身处一座古老的城堡之中。这座城堡有 $n$ 间大厅与 $n-1$ 个走廊，并且从一间大厅到另一间的道路有且仅有一条，也就是说，由这个城堡所构造的图实际上是一颗树。 一开始，也就是在第0时刻，Gerald处在第1间大厅里。这个城堡中的某个大厅里放着Gerald想要的珍宝。然而Gerald并不知道珍宝的确切位置。珍宝在任何另n-1间大厅的可能性都是相等的。只有身处其中，Gerald才能确定这件大厅中到底有没有珍宝。如果你成功地让Gerald看到他想要的珍宝....除了可以拿到一个绿色的AC以外你也得不到什么好处。 每条走廊都有着不同的长度，所以走过每条走廊的时间不相等。由于这座城堡修建的时候是无良外包商修的，所以走廊走过2次就塌了。也就是说Gerald得找到一种策略，让他确保能够每个大厅都去一遍。 举个栗子：若使Gerald走到第二、第三、第四...间大厅的时间分别为$t_2,t_3,t_4...$，那么Gerald找到珍宝的平均时间就是$\frac{(t_2+t_3+t_4+...+t_n)}{(n-1)}$。 ## 输入及范围: 第一行为大厅的个数 $n,(2\le n\le 10^5) $ 接下来 $n-1$ 行为对各个走廊的描述，包括: 走廊连接的两个大厅 $a_i$ 与 $b_i$ 走过走廊所需要的时间 $t_i$ 再次提醒，Gerald一开始站在1号大厅 ## 输出格式 输出一个实数，即Gerald找到珍宝所需时间的期望值，允许不超过 $10^{-6}$ 的误差