Space Rescuers

题意翻译

三维空间里有n个点，求一个点，使距离最远的点距离最小。

题目描述

The Galaxy contains $ n $ planets, there are many different living creatures inhabiting each planet. And each creature can get into troubles! Space rescuers know it perfectly well and they are always ready to help anyone who really needs help. All you need to do is call for them. Now the space rescuers plan to build the largest in the history of the Galaxy rescue station; however, the rescue station's location is yet to be determined. As some cases are real emergencies, the rescuers want to find such a point in the Galaxy from which it would be possible to get to the remotest planet in the minimum possible time. In other words, the rescuers need such point in the space that the distance between it and the planet remotest from it was minimal (if we compare this point with all other possible points in the space). Unfortunately, the rescuers can't sole this problem. As the planets are quite remote from each other, they can be considered as points in Euclidean three-dimensional space. The distance between points $ (x_{i},y_{i},z_{i}) $ and $ (x_{j},y_{j},z_{j}) $ can be calculated by the formula 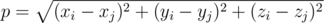. The rescue station can be positioned in any point in the space. It can also coincide with some planet. Galaxy is in danger! Save the space rescuers and find the required point for them.

输入输出格式

输入格式

The first line of the input file contains integer $ n $ — the number of planets ( $ 1<=N<=100 $ ). Each of the following $ n $ lines contains information about the planets. The $ i $ -th line contains three integers $ x_{i},y_{i},z_{i} $ — the coordinates of the $ i $ -th planet ( $ -10^{4}<=x_{i},y_{i},z_{i}<=10^{4} $ , $ 1<=i<=n $ ). No two planets coincide.

输出格式

Print on the first line of the output file three space-separated real numbers $ x_{0},y_{0},z_{0} $ — the coordinates for the future base. If there are several solutions, you are allowed to print any of them. The answer will be accepted if the distance from this point to the remotest planet will differ from the juries' variant in no more than $ 10^{-6} $ in absolute or relative value.

输入输出样例

输入样例 #1

5
5 0 0
-5 0 0
0 3 4
4 -3 0
2 2 -2

输出样例 #1

0.000 0.000 0.000

题意翻译

三维空间里有n个点，求一个点，使距离最远的点距离最小。