Plumber

题意翻译

### 题目描述 小约翰励志成为一名管道工！今天他画了一个包含 $n$ 行 $m$ 列的网格。 在每个单元格中，他将画一段管道。他只能画四种部分管道，使用 1 至 4 标号，如图。 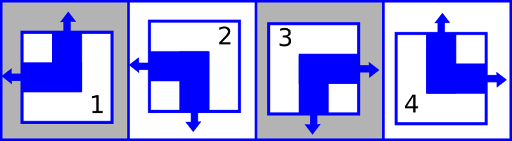 每一个管道都有两端，在上图中使用箭头表示。例如，第 1 幅图的管道的两端分别在上面和左面， 如果网格内有部分管道的末端未连接到另一个管道的末端或网格的边界，则小约翰认为管道系统存在漏洞。下面这幅图就展示了一个在 $1 \times 2$ 的管道组中一个有漏洞的连接和没有漏洞的连接。 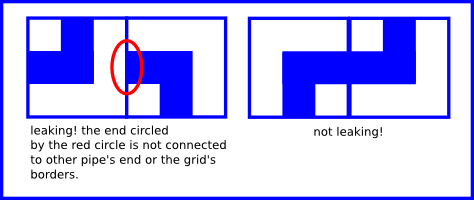 现在给你一个小约翰已经完成部分的管道组。每一个网格中要么有按要求填充的管道，要么没有被填充。您需要找出可组成多少个没有漏洞的管道。将结果取余 $10^6 +3$。 需要注意的是，网格不允许旋转或翻转。因此仅当其中之一水平或垂直旋转或翻转时才相同的两个配置被视为两种不同的方法。 ### 输入格式 第一行输入 $n$，$m$（$1 <= n,m$，$n \times m <= 5 \times 10^5$），表示行数和列数。 接下来 $n$ 行，每行一个字符，解释小约翰已经完成的部分管道，和需要完成的管道。 用 1 ~ 4 表示已经完成的管道，“.”表示未完成的管道。 ### 输出格式 输出最多能有多少种无漏洞的的管道。如果没有，输出 0；否则，将答案取余 $10^6 + 3$ ### 说明提示 ##### 样例 1 解释 网格初始配置如图。 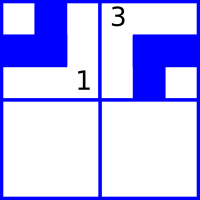 所以最终无漏洞配置只有两种，如下图。 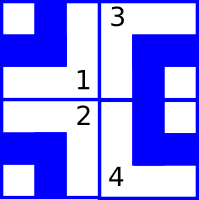  ##### 样例 2 解释 小约翰已完成的管道已经有漏洞了，所以无法拼成无漏洞的管道组。 ##### 样例 3 解释 只有一种方法，如图。  **严格遵照原文，未加改动** 翻译者：[瀛洲仙子](https://www.luogu.com.cn/user/517637)，[郭梁](https://www.luogu.com.cn/user/284186) 提交者：[瀛洲仙子](https://www.luogu.com.cn/user/517637)

题目描述

Little John aspires to become a plumber! Today he has drawn a grid consisting of $ n $ rows and $ m $ columns, consisting of $ n×m $ square cells. In each cell he will draw a pipe segment. He can only draw four types of segments numbered from $ 1 $ to $ 4 $ , illustrated as follows: Each pipe segment has two ends, illustrated by the arrows in the picture above. For example, segment $ 1 $ has ends at top and left side of it. Little John considers the piping system to be leaking if there is at least one pipe segment inside the grid whose end is not connected to another pipe's end or to the border of the grid. The image below shows an example of leaking and non-leaking systems of size $ 1×2 $ . Now, you will be given the grid that has been partially filled by Little John. Each cell will either contain one of the four segments above, or be empty. Find the number of possible different non-leaking final systems after Little John finishes filling all of the empty cells with pipe segments. Print this number modulo $ 1000003 $ ( $ 10^{6}+3 $ ). Note that rotations or flipping of the grid are not allowed and so two configurations that are identical only when one of them has been rotated or flipped either horizontally or vertically are considered two different configurations.

输入输出格式

输入格式

The first line will contain two single-space separated integers $ n $ and $ m $ ( $ 1<=n,m,n·m<=5·10^{5} $ ) — the number of rows and columns respectively. Then $ n $ lines follow, each contains exactly $ m $ characters — the description of the grid. Each character describes a cell and is either one of these: - "1" - "4" — a pipe segment of one of four types as described above - "." — an empty cell

输出格式

Print a single integer denoting the number of possible final non-leaking pipe systems modulo $ 1000003 $ ( $ 10^{6}+3 $ ). If there are no such configurations, print $ 0 $ .

输入输出样例

输入样例 #1

2 2
13
..

输出样例 #1

2

输入样例 #2

3 1
1
4
.

输出样例 #2

0

输入样例 #3

2 2
3.
.1

输出样例 #3

1

说明

For the first example, the initial configuration of the grid is as follows. The only two possible final non-leaking pipe configurations are as follows:  For the second example, the initial grid is already leaking, so there will be no final grid that is non-leaking. For the final example, there's only one possible non-leaking final grid as follows.