Before Exam

题意翻译

再过几分钟，Vasya 在大学里的第一场考试就要开始了。这可是数学分析考试。当然，现在 Vasya 脑中只有一件事情：他与考官相谈的结果会是…… 一名考生需要学习 $n$ 个定理。有 $k$ 张卡片。考试时，每个定理会被写到 $k$ 张卡片中的至多一张上，每张卡片上会写下 $\lfloor\frac{n}{k}\rfloor$ 个互不相同的定理（换言之，有 $n-k\cdot\lfloor\frac{n}{k}\rfloor$ 个定理没有被考到）。在考试时，每名学生会拿到一张卡片。不同的学生可能拿到同一张卡片。 我们不知道每个定理被写到了哪张卡片上，不过排在 Vasya 之前的考生都向他透露了他们拿到的卡片上的定理。Vasya 估计他对第 $i$ 个定理的熟练度为 $a_i$。他对一张卡片的熟练度为他对卡片上所有定理的熟练度的平均值。Vasya 想通过从其他考生处取得的数据计算他对他拿到的卡片的熟练度有可能达到的最小值与最大值。不幸的是，Vasya 没时间了，只能让您帮他。 --- 第一行，两个正整数 $n$、$k$（$1 \le k \le n \le 100$），表示定理数量与卡片数量。 第二行，$n$ 个非负整数 $a_1,a_2,\dots,a_n$，其中 $a_i$（$0\le a_i \le 100$） 表示 Vasya 对第 $i$ 个定理的熟练度。 第三行，一个非负整数 $q$（$0\leq q\leq 100$），表示排在 Vasya 之前的考生数量。 接下来 $q$ 行，每行 $\lfloor\frac{n}{k}\rfloor$ 个 $1$、$n$ 之间的互不相同的整数，表示一名考生拿到的卡片上的定理的编号。两名考生拿到的定理要么没有交集，要么完全一样（顺序可能不同）。 --- 输出两个实数，分别表示 Vasya 对他的卡片的熟练度的可能的最小值和最大值，绝对或相对误差不超过 $10^{-6}$。

题目描述

Vasya is about to take his first university exam in about several minutes. And it's not just some ordinary exam, it's on mathematical analysis. Of course, right now Vasya can only think of one thing: what the result of his talk with the examiner will be... To prepare for the exam, one has to study proofs of $ n $ theorems. It is known that there will be $ k $ examination cards on the exam and each card contains 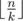 distinct theorems. Besides, no theorem is mentioned in more than one card (that is, 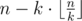 theorems won't be mentioned in any card). During the exam several students may get the same card. We do not know the exact way theorems are distributed by cards, however the students that took the exam before Vasya told him what theorems their cards contained. Vasya evaluates his level of proficiency in the $ i $ -th theorem by some number $ a_{i} $ . The level of proficiency in some card is the average of the levels of proficiency in the theorems that are included in the card. Now Vasya wants to know the minimally and maximally possible levels of his proficiency in the card he gets on the exam. Vasya wants to determine it by the data he has collected from other students. Unfortunately, Vasya has no time left to do the math and he asked you to help him.

输入输出格式

输入格式

The first line contains two integers $ n $ and $ k $ ( $ 1<=k<=n<=100 $ ) — the number of theorems and the number of cards correspondingly. The second line contains $ n $ integers $ a_{i} $ ( $ 0<=a_{i}<=100 $ ), the $ i $ -th number ( $ 1<=i<=n $ ) corresponds to Vasya's proficiency in the $ i $ -th theorem. The third line contains number $ q $ ( $ 0<=q<=100 $ ) — the number of people that have taken the exam before Vasya. Each of the following $ q $ lines contains the description of a student's card: 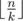 integers from $ 1 $ to $ n $ inclusive. They are the numbers of theorems included in the card in the order in which they are enumerated in the input data. The numbers are given in an arbitrary order. It is guaranteed that the given cards are valid (that is, that all theorems in one card are different and that different people get cards that either don't contain the same theorems or coincide up to the theorems' permutation).

输出格式

Print two real numbers, representing Vasya's minimum and maximum proficiency in the card he will get on the exam. The absolute or relative error should not exceed $ 10^{-6} $ .

输入输出样例

输入样例 #1

7 3
7 15 0 19 10 5 12
2
1 6
7 4

输出样例 #1

5.0000000000 15.5000000000

输入样例 #2

4 2
10 8 1 17
2
2 3
3 2

输出样例 #2

4.5000000000 13.5000000000

说明

Let's analyze the first sample. Vasya's proficiency in the cards whose content he already knows equals $ 6 $ and $ 15.5 $ correspondingly. The three theorems that are left are only enough to make one exam card. If we consider all possible variants of theorems included in the card we can see that in the best case scenario Vasya gets the card that contains theorems $ 4 $ and $ 7 $ (his proficiency would equal $ 15.5 $ ) and in the worst case scenario he gets theorems $ 3 $ and $ 5 $ (his proficiency would equal $ 5 $ ). The $ ⌊\ x⌋ $ operation denotes taking integer part of real number $ x $ (rounding down).