E-reader Display

题意翻译

给定一个 $n \times n$ 的正方形，初始时每个点都是 `0`。当接收到 $(x,y)$ 的命令时，$(x,x) \rarr (x,y)$ 和 $(x,y) \rarr (y,y)$ 段（包括两端点）中的每个点均发生反转（`1` 变 `0`，`0` 变 `1`）。 计算使输入的表每个点都变为 0 所需的最少命令数 $s$，并输出。 **【输入格式】** 第一行一个正整数 $n$，接下来 $n$ 行描述一个 $n \times n$ 的由 ```0``` 或 ```1``` 组成的矩形。 **【输出格式】** 一行一个整数，表示把矩形改为全 ```0``` 的最少操作步数。 **【数据范围】** $1 \leq n \leq 2 \times 10^3$，输入的数组只由 ```0``` 或 ```1``` 组成。

题目描述

After years of hard work scientists invented an absolutely new e-reader display. The new display has a larger resolution, consumes less energy and its production is cheaper. And besides, one can bend it. The only inconvenience is highly unusual management. For that very reason the developers decided to leave the e-readers' software to programmers. The display is represented by $ n×n $ square of pixels, each of which can be either black or white. The display rows are numbered with integers from $ 1 $ to $ n $ upside down, the columns are numbered with integers from $ 1 $ to $ n $ from the left to the right. The display can perform commands like " $ x,y $ ". When a traditional display fulfills such command, it simply inverts a color of $ (x,y) $ , where $ x $ is the row number and $ y $ is the column number. But in our new display every pixel that belongs to at least one of the segments $ (x,x)-(x,y) $ and $ (y,y)-(x,y) $ (both ends of both segments are included) inverts a color. For example, if initially a display $ 5×5 $ in size is absolutely white, then the sequence of commands $ (1,4) $ , $ (3,5) $ , $ (5,1) $ , $ (3,3) $ leads to the following changes: 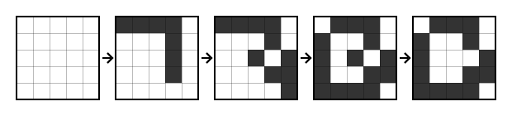You are an e-reader software programmer and you should calculate minimal number of commands needed to display the picture. You can regard all display pixels as initially white.

输入输出格式

输入格式

The first line contains number $ n $ ( $ 1<=n<=2000 $ ). Next $ n $ lines contain $ n $ characters each: the description of the picture that needs to be shown. "0" represents the white color and "1" represents the black color.

输出格式

Print one integer $ z $ — the least number of commands needed to display the picture.

输入输出样例

输入样例 #1

5
01110
10010
10001
10011
11110

输出样例 #1

4

题意翻译

给定一个 $n \times n$ 的正方形，初始时每个点都是 `0`。当接收到 $(x,y)$ 的命令时，$(x,x) \rarr (x,y)$ 和 $(x,y) \rarr (y,y)$ 段（包括两端点）中的每个点均发生反转（`1` 变 `0`，`0` 变 `1`）。 计算使输入的表每个点都变为 0 所需的最少命令数 $s$，并输出。 **【输入格式】** 第一行一个正整数 $n$，接下来 $n$ 行描述一个 $n \times n$ 的由 ```0``` 或 ```1``` 组成的矩形。 **【输出格式】** 一行一个整数，表示把矩形改为全 ```0``` 的最少操作步数。 **【数据范围】** $1 \leq n \leq 2 \times 10^3$，输入的数组只由 ```0``` 或 ```1``` 组成。