Smart Cheater

题意翻译

Nvodsk 的公交 $62$ 路的路线有 $n$ 站 ( $1$ 站在前面， $n$ 站在最后)。停止点定位在一条直线上，其坐标为 $0=x_{1}<x_{2}<…<x_{n}$ 。 每天都有 $m$ 人乘坐公交车 $62$ 路。我们知道每个人上车的站号和下车的站号。一张从 $a$ 站到 $b$ 站的票 ( $a<b$ ) 的价格是 $x_{b}-x_{A}$ 卢布。但是，售票员最多只能选择一段“不卖票”。我们的意思是售票员应该选择 $C$ 和 $D$ ( $C <= D$ ) ，然后为 【 $A$ ， $C$ 】 和 【 $D$ ， $B$ 】 售票，否则根本不售票。售票员和乘客平分节省下来的钱。售票员的“未纳税收入”有时会被检查打断，当公共汽车行驶在两个连续站点之间的某个路段时。检票员会对每一位没有这段线路车票的乘客罚款 $c$ 卢布。 你知道如何协调所有 $x_{i}$ 站;第 $i$ 位乘客上下车的站数 $a_{i}$ 和 $b_{i}$ ( $a_{i}<b_{i}$ ) ;总罚款 $c$ 卢布;还有 $p_{i}$ 在 $i$ 第一个和 $i+1$ 第一个停止之间的段上检查的概率。售票员请你帮他制定一个售票计划，使他的利润的数学期望值最大化。 ## 输入格式 第一行包含三个整数 $n$ ， $m$ 和 $c$ ( $2<=n<=150000$ , $1<=m<=300000$ , $1<=c<=10000$ )。 下一行包含n整数 $x_{i}$ ( $0<=x_{i}<=10^{9}$ ， $x_{1}=0$ ， $x_{i}<x_{i+1}$ ) 公共汽车路线上站点的坐标。 第三行包含 $n-1$ 个整数 $p_{i}$ ( $0<=p_{i}<=100$ )在 $i$ 站和 $i+1$ 站之间的段上检查的概率的百分比。 然后沿着描述巴士乘客 $m$ 的线路走。每行包含两个整数 $a_{i}$ 和 $b_{i}$ ( $1<=a_{i}<b_{i}<=n$ ) —第 $i$ 号乘客上下车的站数。 ## 输出格式 输出单个实数即售票员的最大数学期望利润。如果你的答案的绝对或相对误差不超过 $10^-6$ ，你的答案将被认为是正确的。 假设你的答案是 $a$ 美元，陪审团的答案是 $b$ 美元。检查程序将认为你的答案正确，如果第一个和第三个乘客的票价从 $1$ 美元到 $2$ 美元不等。第二位乘客没有买票。在 $1$ 美元到 $2$ 美元的区间总会有检查，但两名乘客都有票。在 $2$ 美元到 $3$ 美元之间从来没有检查，这就是为什么第二名乘客可以侥幸逃脱。总利润将是 $（ 0+90/2+90/2)=90$ 美元。

题目描述

I guess there's not much point in reminding you that Nvodsk winters aren't exactly hot. That increased the popularity of the public transport dramatically. The route of bus $ 62 $ has exactly $ n $ stops (stop $ 1 $ goes first on its way and stop $ n $ goes last). The stops are positioned on a straight line and their coordinates are $ 0=x_{1}&lt;x_{2}&lt;...&lt;x_{n} $ . Each day exactly $ m $ people use bus $ 62 $ . For each person we know the number of the stop where he gets on the bus and the number of the stop where he gets off the bus. A ticket from stop $ a $ to stop $ b $ ( $ a&lt;b $ ) costs $ x_{b}-x_{a} $ rubles. However, the conductor can choose no more than one segment NOT TO SELL a ticket for. We mean that conductor should choose C and D (С <= D) and sell a ticket for the segments \[ $ A $ , $ C $ \] and \[ $ D $ , $ B $ \], or not sell the ticket at all. The conductor and the passenger divide the saved money between themselves equally. The conductor's "untaxed income" is sometimes interrupted by inspections that take place as the bus drives on some segment of the route located between two consecutive stops. The inspector fines the conductor by $ c $ rubles for each passenger who doesn't have the ticket for this route's segment. You know the coordinated of all stops $ x_{i} $ ; the numbers of stops where the $ i $ -th passenger gets on and off, $ a_{i} $ and $ b_{i} $ ( $ a_{i}&lt;b_{i} $ ); the fine $ c $ ; and also $ p_{i} $ — the probability of inspection on segment between the $ i $ -th and the $ i+1 $ -th stop. The conductor asked you to help him make a plan of selling tickets that maximizes the mathematical expectation of his profit.

输入输出格式

输入格式

The first line contains three integers $ n $ , $ m $ and $ c $ ( $ 2<=n<=150000 $ , $ 1<=m<=300000 $ , $ 1<=c<=10000 $ ). The next line contains $ n $ integers $ x_{i} $ ( $ 0<=x_{i}<=10^{9} $ , $ x_{1}=0 $ , $ x_{i}&lt;x_{i+1} $ ) — the coordinates of the stops on the bus's route. The third line contains $ n-1 $ integer $ p_{i} $ ( $ 0<=p_{i}<=100 $ ) — the probability of inspection in percents on the segment between stop $ i $ and stop $ i+1 $ . Then follow $ m $ lines that describe the bus's passengers. Each line contains exactly two integers $ a_{i} $ and $ b_{i} $ ( $ 1<=a_{i}&lt;b_{i}<=n $ ) — the numbers of stops where the $ i $ -th passenger gets on and off.

输出格式

Print the single real number — the maximum expectation of the conductor's profit. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ . Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct, if .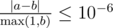

输入输出样例

输入样例 #1

3 3 10
0 10 100
100 0
1 2
2 3
1 3

输出样例 #1

90.000000000

输入样例 #2

10 8 187
0 10 30 70 150 310 630 1270 2550 51100
13 87 65 0 100 44 67 3 4
1 10
2 9
3 8
1 5
6 10
2 7
4 10
4 5

输出样例 #2

76859.990000000

说明

A comment to the first sample: The first and third passengers get tickets from stop $ 1 $ to stop $ 2 $ . The second passenger doesn't get a ticket. There always is inspection on the segment $ 1 $ - $ 2 $ but both passengers have the ticket for it. There never is an inspection on the segment $ 2 $ - $ 3 $ , that's why the second passenger gets away with the cheating. Our total profit is $ (0+90/2+90/2)=90 $ .

题意翻译

## 题目描述 有条路，路上有 $n$ 个车站，车站 $i$ 位于 $x_i$，每天有 $m$ 个人坐车，第 $j$ 个人从 $a_j$ 坐到 $b_j$。 从车站 $i$ 坐到车站 $j$ 的票价为 $x_j-x_i(i<j)$ 卢布。 现在售票员想要多拿点钱，对于一个乘客，假设从车站 $A$ 坐到车站 $B$，则售票员可以选择两个车站编号 $C,D (A\leqslant C\leqslant D \leqslant B)$ 免去该乘客 $\left[C,D\right]$ 这一段的路费，也可以选择不免去任何路费。若免去一部分路费，那么这些免去的路费将会平均分给售票员和这位乘客作为利润。每一个乘客的 $C,D$ 可以不同。 相应的，每两个相邻车站 $i,i+1$ 的路段都有 $p_i$ 的概率被检查，如果被检查且存在没有购买这个路段车票的乘客，则每有一个没有购买这个路段车票的乘客，售票员都会被罚款 $c$ 卢布（乘客不管了，反正不影响答案）。 求售票员获得利润的最大期望。 ## 输入格式 第一行三个整数：$n,m,c$，表示车站数，总共的乘客数与罚款。 第二行 $n$ 个整数，第 $i$ 个整数表示第 $i$ 个车站的位置。 第三行 $n-1$ 个整数 $p_i$，表示 $i$ 到 $i+1$ 这一路段被检查概率的**百分比**。 接下来 $m$ 行，每一行两个整数 $a_i,b_i$，表示第 $i$ 个乘客上下车的车站编号。 ## 输出格式 一行一个浮点数 $ans$，要求与真实答案的差小于 $10^{-6}$。 ## 数据范围 $0 = x_1<x_2<\dots<x_n \leqslant 10^9$ $2\leqslant n \leqslant 150000, 1\leqslant m \leqslant 300000, 1\leqslant c \leqslant 10000$ $0\leqslant p_i \leqslant 100$ ## 样例解释 样例 1： 第一位和第三位乘客都购买了 $[1,2]$ 路段的车票。 第二位和第三位乘客 $[2,3]$ 这一路段的路费被免去，且一定不会被检查（$p_2=0$） 总利润期望即为 $0 + \frac{90}2 + \frac{90}2 = 90$