Number Challenge

题意翻译

题意:记d(i)表示i的约数个数，输入a,b,c; 求 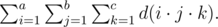%mod(1073741824($2^{30}$))的值。 Translated by @Roots

题目描述

Let's denote $ d(n) $ as the number of divisors of a positive integer $ n $ . You are given three integers $ a $ , $ b $ and $ c $ . Your task is to calculate the following sum: 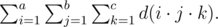Find the sum modulo $ 1073741824 $ $ (2^{30}) $ .

输入输出格式

输入格式

The first line contains three space-separated integers $ a $ , $ b $ and $ c $ ( $ 1<=a,b,c<=2000 $ ).

输出格式

Print a single integer — the required sum modulo $ 1073741824 $ $ (2^{30}) $ .

输入输出样例

输入样例 #1

2 2 2

输出样例 #1

20

输入样例 #2

4 4 4

输出样例 #2

328

输入样例 #3

10 10 10

输出样例 #3

11536

说明

For the first example. - $ d(1·1·1)=d(1)=1 $ ; - $ d(1·1·2)=d(2)=2 $ ; - $ d(1·2·1)=d(2)=2 $ ; - $ d(1·2·2)=d(4)=3 $ ; - $ d(2·1·1)=d(2)=2 $ ; - $ d(2·1·2)=d(4)=3 $ ; - $ d(2·2·1)=d(4)=3 $ ; - $ d(2·2·2)=d(8)=4 $ . So the result is $ 1+2+2+3+2+3+3+4=20 $ .

题意翻译

题意:记d(i)表示i的约数个数，输入a,b,c; 求 %mod(1073741824($2^{30}$))的值。 Translated by @Roots