Easy Number Challenge

题意翻译

给定 $\text{a, b, c}$ 三个数，$d_i$ 表示 $\text{i}$ 的因子的个数。求 $\sum^{a}_{i=1} \sum^{b}_{j=1} \sum^{c}_{k=1} d \left(i \cdot j \cdot k \right)$ 的值。结果对1073741824 ( $2^{30}$ )取模。

题目描述

Let's denote $ d(n) $ as the number of divisors of a positive integer $ n $ . You are given three integers $ a $ , $ b $ and $ c $ . Your task is to calculate the following sum: 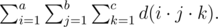Find the sum modulo $ 1073741824 $ $ (2^{30}) $ .

输入输出格式

输入格式

The first line contains three space-separated integers $ a $ , $ b $ and $ c $ ( $ 1<=a,b,c<=100 $ ).

输出格式

Print a single integer — the required sum modulo $ 1073741824 $ $ (2^{30}) $ .

输入输出样例

输入样例 #1

2 2 2

输出样例 #1

20

输入样例 #2

5 6 7

输出样例 #2

1520

说明

For the first example. - $ d(1·1·1)=d(1)=1 $ ; - $ d(1·1·2)=d(2)=2 $ ; - $ d(1·2·1)=d(2)=2 $ ; - $ d(1·2·2)=d(4)=3 $ ; - $ d(2·1·1)=d(2)=2 $ ; - $ d(2·1·2)=d(4)=3 $ ; - $ d(2·2·1)=d(4)=3 $ ; - $ d(2·2·2)=d(8)=4 $ . So the result is $ 1+2+2+3+2+3+3+4=20 $ .