Maximum Xor Secondary

题意翻译

题目大意： 给出一个长为n的正整数序列。定义一个序列的所有数异或的结果为其最大值和次大值的异或值。求在此序列的所有子串（即要求连续一段区间）中价值最大是多少。 输入： 第一行一个整数n($1≤n≤10^5$),表示序列长度。 第二行n个由空格隔开的正整数$s_i$(($1≤s_i≤10^9$))，为序列元素。 输出仅一个整数，即最大异或和。

题目描述

Bike loves looking for the second maximum element in the sequence. The second maximum element in the sequence of distinct numbers $ x_{1},x_{2},...,x_{k} $ $ (k&gt;1) $ is such maximum element $ x_{j} $ , that the following inequality holds: 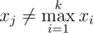. The lucky number of the sequence of distinct positive integers $ x_{1},x_{2},...,x_{k} $ $ (k&gt;1) $ is the number that is equal to the bitwise excluding OR of the maximum element of the sequence and the second maximum element of the sequence. You've got a sequence of distinct positive integers $ s_{1},s_{2},...,s_{n} $ $ (n&gt;1) $ . Let's denote sequence $ s_{l},s_{l+1},...,s_{r} $ as $ s[l..r] $ $ (1<=l&lt;r<=n) $ . Your task is to find the maximum number among all lucky numbers of sequences $ s[l..r] $ . Note that as all numbers in sequence $ s $ are distinct, all the given definitions make sence.

输入输出格式

输入格式

The first line contains integer $ n $ $ (1&lt;n<=10^{5}) $ . The second line contains $ n $ distinct integers $ s_{1},s_{2},...,s_{n} $ $ (1<=s_{i}<=10^{9}) $ .

输出格式

Print a single integer — the maximum lucky number among all lucky numbers of sequences $ s[l..r] $ .

输入输出样例

输入样例 #1

5
5 2 1 4 3

输出样例 #1

7

输入样例 #2

5
9 8 3 5 7

输出样例 #2

15

说明

For the first sample you can choose $ s[4..5]={4,3} $ and its lucky number is $ (4 xor 3)=7 $ . You can also choose $ s[1..2] $ . For the second sample you must choose $ s[2..5]={8,3,5,7} $ .