Rectangle Puzzle II

题意翻译

在 $(0, 0) \sim (n, m)$ 中找一个最大子矩形，使其包含定点 $(x, y)$，而且 $\frac{x_2 - x_1}{y_2 - y_1} = \frac{a}{b}$。如果有多个解，输出最接近 $(x, y)$ 的矩形。如果仍有多个解决方案，按字典顺序排列的最小解决方案。　　

题目描述

You are given a rectangle grid. That grid's size is $ n×m $ . Let's denote the coordinate system on the grid. So, each point on the grid will have coordinates — a pair of integers $ (x,y) $ $ (0<=x<=n,0<=y<=m) $ . Your task is to find a maximum sub-rectangle on the grid $ (x_{1},y_{1},x_{2},y_{2}) $ so that it contains the given point $ (x,y) $ , and its length-width ratio is exactly $ (a,b) $ . In other words the following conditions must hold: $ 0<=x_{1}<=x<=x_{2}<=n $ , $ 0<=y_{1}<=y<=y_{2}<=m $ , 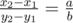. The sides of this sub-rectangle should be parallel to the axes. And values $ x_{1},y_{1},x_{2},y_{2} $ should be integers. 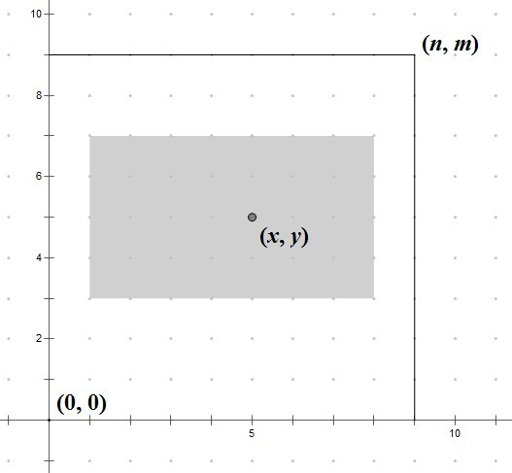If there are multiple solutions, find the rectangle which is closest to $ (x,y) $ . Here "closest" means the Euclid distance between $ (x,y) $ and the center of the rectangle is as small as possible. If there are still multiple solutions, find the lexicographically minimum one. Here "lexicographically minimum" means that we should consider the sub-rectangle as sequence of integers $ (x_{1},y_{1},x_{2},y_{2}) $ , so we can choose the lexicographically minimum one.

输入输出格式

输入格式

The first line contains six integers $ n,m,x,y,a,b $ $ (1<=n,m<=10^{9},0<=x<=n,0<=y<=m,1<=a<=n,1<=b<=m) $ .

输出格式

Print four integers $ x_{1},y_{1},x_{2},y_{2} $ , which represent the founded sub-rectangle whose left-bottom point is $ (x_{1},y_{1}) $ and right-up point is $ (x_{2},y_{2}) $ .

输入输出样例

输入样例 #1

9 9 5 5 2 1

输出样例 #1

1 3 9 7

输入样例 #2

100 100 52 50 46 56

输出样例 #2

17 8 86 92

题意翻译

在 $(0, 0) \sim (n, m)$ 中找一个最大子矩形，使其包含定点 $(x, y)$，而且 $\frac{x_2 - x_1}{y_2 - y_1} = \frac{a}{b}$。如果有多个解，输出最接近 $(x, y)$ 的矩形。如果仍有多个解决方案，按字典顺序排列的最小解决方案。