Sereja and Periods

题意翻译

## 题目描述 设$[s,t]$（$s$为一个字符串，$t$为正整数）为字符串$s$重复$t$次后的新字符串 再设当字符串$s$中删去部分字符后，得到字符串$t$，则称字符串$s$包含$t$ 现在Sereja有两个字符串，可以表示为$w=[a,b]$和$q=[c,d]$，求使得$w$包含$[q,p]$的最大的正整数$p$ ## 输入格式 第一行为两个正整数$b,d$，其中$1\le b,d\le 10^7$ 第二行和第三行方便为字符串$a$和字符串$c$，其中$0<|a|,|c|\le 100$，且仅包含小写英文字母 ## 输出格式 输出唯一一个整数$p$，为求使得$[a,b]$包含$[[c,d],p]$的最大的正整数$p$ 此外，如果没有合法的$p$，请输出$0$

题目描述

Let's introduce the designation 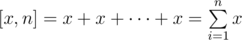, where $ x $ is a string, $ n $ is a positive integer and operation " $ + $ " is the string concatenation operation. For example, $ [abc,2]=abcabc $ . We'll say that string $ s $ can be obtained from string $ t $ , if we can remove some characters from string $ t $ and obtain string $ s $ . For example, strings $ ab $ and $ aсba $ can be obtained from string $ xacbac $ , and strings $ bx $ and $ aaa $ cannot be obtained from it. Sereja has two strings, $ w=[a,b] $ and $ q=[c,d] $ . He wants to find such maximum integer $ p $ $ (p&gt;0) $ , that $ [q,p] $ can be obtained from string $ w $ .

输入输出格式

输入格式

The first line contains two integers $ b $ , $ d $ $ (1<=b,d<=10^{7}) $ . The second line contains string $ a $ . The third line contains string $ c $ . The given strings are not empty and consist of lowercase English letters. Their lengths do not exceed $ 100 $ .

输出格式

In a single line print an integer — the largest number $ p $ . If the required value of $ p $ doesn't exist, print 0.

输入输出样例

输入样例 #1

10 3
abab
bab

输出样例 #1

3

题意翻译

## 题目描述 设$[s,t]$（$s$为一个字符串，$t$为正整数）为字符串$s$重复$t$次后的新字符串 再设当字符串$s$中删去部分字符后，得到字符串$t$，则称字符串$s$包含$t$ 现在Sereja有两个字符串，可以表示为$w=[a,b]$和$q=[c,d]$，求使得$w$包含$[q,p]$的最大的正整数$p$ ## 输入格式 第一行为两个正整数$b,d$，其中$1\le b,d\le 10^7$ 第二行和第三行方便为字符串$a$和字符串$c$，其中$0<|a|,|c|\le 100$，且仅包含小写英文字母 ## 输出格式 输出唯一一个整数$p$，为求使得$[a,b]$包含$[[c,d],p]$的最大的正整数$p$ 此外，如果没有合法的$p$，请输出$0$