Summer Homework

题意翻译

- 在这里，我们用 $f_i$ 表示第 $i$ 个斐波那契数（$f_0=1,f_1=1,f_i=f_{i-1}+f_{i-2}(i\ge 2)$）。 - 给定 $n$ 个数的序列 $a$。$m$ 次操作。操作有三种： 1. `1 x v`：将 $a_x$ 赋值为 $v$。 2. `2 l r`：求 $$\sum_{x=0}^{r-l}(f_x\cdot a_{l+x})\bmod 10^9$$ 3. `3 l r d`：将 $a_l\sim a_r$ 加上 $d$。 - $1\le n,m\le 2\times 10^5$，$0\le a_i,v,d\le 10^5$。

题目描述

By the age of three Smart Beaver mastered all arithmetic operations and got this summer homework from the amazed teacher: You are given a sequence of integers $ a_{1},a_{2},...,a_{n} $ . Your task is to perform on it $ m $ consecutive operations of the following type: 1. For given numbers $ x_{i} $ and $ v_{i} $ assign value $ v_{i} $ to element $ a_{xi} $ . 2. For given numbers $ l_{i} $ and $ r_{i} $ you've got to calculate sum 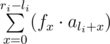, where $ f_{0}=f_{1}=1 $ and at $ i>=2 $ : $ f_{i}=f_{i-1}+f_{i-2} $ . 3. For a group of three numbers $ l_{i} $ $ r_{i} $ $ d_{i} $ you should increase value $ a_{x} $ by $ d_{i} $ for all $ x $ $ (l_{i}<=x<=r_{i}) $ . Smart Beaver planned a tour around great Canadian lakes, so he asked you to help him solve the given problem.

输入输出格式

输入格式

The first line contains two integers $ n $ and $ m $ ( $ 1<=n,m<=2·10^{5} $ ) — the number of integers in the sequence and the number of operations, correspondingly. The second line contains $ n $ integers $ a_{1},a_{2},...,a_{n} $ ( $ 0<=a_{i}<=10^{5} $ ). Then follow $ m $ lines, each describes an operation. Each line starts with an integer $ t_{i} $ ( $ 1<=t_{i}<=3 $ ) — the operation type: - if $ t_{i}=1 $ , then next follow two integers $ x_{i} $ $ v_{i} $ ( $ 1<=x_{i}<=n,0<=v_{i}<=10^{5} $ ); - if $ t_{i}=2 $ , then next follow two integers $ l_{i} $ $ r_{i} $ ( $ 1<=l_{i}<=r_{i}<=n $ ); - if $ t_{i}=3 $ , then next follow three integers $ l_{i} $ $ r_{i} $ $ d_{i} $ ( $ 1<=l_{i}<=r_{i}<=n,0<=d_{i}<=10^{5} $ ). The input limits for scoring $ 30 $ points are (subproblem E1): - It is guaranteed that $ n $ does not exceed $ 100 $ , $ m $ does not exceed $ 10000 $ and there will be no queries of the $ 3 $ -rd type. The input limits for scoring $ 70 $ points are (subproblems E1+E2): - It is guaranteed that there will be queries of the $ 1 $ -st and $ 2 $ -nd type only. The input limits for scoring $ 100 $ points are (subproblems E1+E2+E3): - No extra limitations.

输出格式

For each query print the calculated sum modulo $ 1000000000 $ $ (10^{9}) $ .

输入输出样例

输入样例 #1

5 5
1 3 1 2 4
2 1 4
2 1 5
2 2 4
1 3 10
2 1 5

输出样例 #1

12
32
8
50

输入样例 #2

5 4
1 3 1 2 4
3 1 4 1
2 2 4
1 2 10
2 1 5

输出样例 #2

12
45