Counting Skyscrapers

题意翻译

有一排楼，数量 $[2,314!]$。（反正就是很多） 每一栋大楼有一个正整数高度，为 $i$ 的概率为 $\frac{1}{2^i}$。 在任意对大楼间每层都有通道，但通道满足比他经过的楼（不包含起始的两个楼）要高。 设楼的 $i$ 高度为 $h_i$，即楼 $i, j$ 间的通道高度 $h$ 满足 $h > \max_{k=i}^j \{ h_k \}$。 给定一个 $h$，Alice 和 Bob 分别有两个计数器 $A, B$。$A, B$ 初始都等于 $1$。 Alice 的从左向右走，每经过一栋楼 $A \gets A + 1$，最后 $A$ 为楼的总数。 Bob 的计数方法是每到一个楼，都会从最高但高度小于等于 $h$ 的通道向右到通道的另一端。设这个通道高度为 $k$，则 $B \gets B + 2^k$。 （图例见原题）图中上方是 $B$ 的变化，下方是 $A$ 的变化。 现在给你 $A$ 的值让你推算 $B$ 的期望值。 或者给你 $B$ 和 $h$ 让你推算 $A$ 的期望值。

题目描述

A number of skyscrapers have been built in a line. The number of skyscrapers was chosen uniformly at random between $ 2 $ and $ 314! $ (314 factorial, a very large number). The height of each skyscraper was chosen randomly and independently, with height $ i $ having probability $ 2^{-i} $ for all positive integers $ i $ . The floors of a skyscraper with height $ i $ are numbered $ 0 $ through $ i-1 $ . To speed up transit times, a number of zip lines were installed between skyscrapers. Specifically, there is a zip line connecting the $ i $ -th floor of one skyscraper with the $ i $ -th floor of another skyscraper if and only if there are no skyscrapers between them that have an $ i $ -th floor. Alice and Bob decide to count the number of skyscrapers. Alice is thorough, and wants to know exactly how many skyscrapers there are. She begins at the leftmost skyscraper, with a counter at 1. She then moves to the right, one skyscraper at a time, adding 1 to her counter each time she moves. She continues until she reaches the rightmost skyscraper. Bob is impatient, and wants to finish as fast as possible. He begins at the leftmost skyscraper, with a counter at 1. He moves from building to building using zip lines. At each stage Bob uses the highest available zip line to the right, but ignores floors with a height greater than $ h $ due to fear of heights. When Bob uses a zip line, he travels too fast to count how many skyscrapers he passed. Instead, he just adds $ 2^{i} $ to his counter, where $ i $ is the number of the floor he's currently on. He continues until he reaches the rightmost skyscraper. Consider the following example. There are $ 6 $ buildings, with heights $ 1 $ , $ 4 $ , $ 3 $ , $ 4 $ , $ 1 $ , $ 2 $ from left to right, and $ h=2 $ . Alice begins with her counter at $ 1 $ and then adds $ 1 $ five times for a result of $ 6 $ . Bob begins with his counter at $ 1 $ , then he adds $ 1 $ , $ 4 $ , $ 4 $ , and $ 2 $ , in order, for a result of $ 12 $ . Note that Bob ignores the highest zip line because of his fear of heights ( $ h=2 $ ). 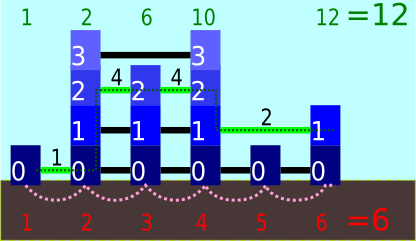Bob's counter is at the top of the image, and Alice's counter at the bottom. All zip lines are shown. Bob's path is shown by the green dashed line and Alice's by the pink dashed line. The floors of the skyscrapers are numbered, and the zip lines Bob uses are marked with the amount he adds to his counter. When Alice and Bob reach the right-most skyscraper, they compare counters. You will be given either the value of Alice's counter or the value of Bob's counter, and must compute the expected value of the other's counter.

输入输出格式

输入格式

The first line of input will be a name, either string "Alice" or "Bob". The second line of input contains two integers $ n $ and $ h $ ( $ 2<=n<=30000 $ , $ 0<=h<=30 $ ). If the name is "Alice", then $ n $ represents the value of Alice's counter when she reaches the rightmost skyscraper, otherwise $ n $ represents the value of Bob's counter when he reaches the rightmost skyscraper; $ h $ represents the highest floor number Bob is willing to use.

输出格式

Output a single real value giving the expected value of the Alice's counter if you were given Bob's counter, or Bob's counter if you were given Alice's counter. You answer will be considered correct if its absolute or relative error doesn't exceed $ 10^{-9} $ .

输入输出样例

输入样例 #1

Alice
3 1

输出样例 #1

3.500000000

输入样例 #2

Bob
2 30

输出样例 #2

2

输入样例 #3

Alice
2572 10

输出样例 #3

3439.031415943

说明

In the first example, Bob's counter has a 62.5% chance of being 3, a 25% chance of being 4, and a 12.5% chance of being 5.

题意翻译

有一排楼，数量 $[2,314!]$。（反正就是很多） 每一栋大楼有一个正整数高度，为 $i$ 的概率为 $\frac{1}{2^i}$。 在任意对大楼间每层都有通道，但通道满足比他经过的楼（不包含起始的两个楼）要高。 设楼的 $i$ 高度为 $h_i$，即楼 $i, j$ 间的通道高度 $h$ 满足 $h > \max_{k=i}^j \{ h_k \}$。 给定一个 $h$，Alice 和 Bob 分别有两个计数器 $A, B$。$A, B$ 初始都等于 $1$。 Alice 的从左向右走，每经过一栋楼 $A \gets A + 1$，最后 $A$ 为楼的总数。 Bob 的计数方法是每到一个楼，都会从最高但高度小于等于 $h$ 的通道向右到通道的另一端。设这个通道高度为 $k$，则 $B \gets B + 2^k$。 （图例见原题）图中上方是 $B$ 的变化，下方是 $A$ 的变化。 现在给你 $A$ 的值让你推算 $B$ 的期望值。 或者给你 $B$ 和 $h$ 让你推算 $A$ 的期望值。