Searching for Graph

题意翻译

#### 给定两个数$n,p$,要求构造一个无向图，并满足以下条件 > 1. 该图正好有 $n*2 + p$ 个边 > 2. 图中不包含自环和重边 > 3. 图中任选$k$个点构成的子图边的数量小于等于 $n*2 + p$ #### 数据范围 > 有$t$组数据，每组之间空行隔开$(t<=5)$ > $5<=n<=24,p >=0, 2*n + p <= \frac{n*(n-1)}{2} $

题目描述

Let's call an undirected graph of $ n $ vertices $ p $ -interesting, if the following conditions fulfill: - the graph contains exactly $ 2n+p $ edges; - the graph doesn't contain self-loops and multiple edges; - for any integer $ k $ ( $ 1<=k<=n $ ), any subgraph consisting of $ k $ vertices contains at most $ 2k+p $ edges. A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices. Your task is to find a $ p $ -interesting graph consisting of $ n $ vertices.

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1<=t<=5 $ ) — the number of tests in the input. Next $ t $ lines each contains two space-separated integers: $ n $ , $ p $ ( $ 5<=n<=24 $ ; $ p>=0 $ ; 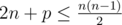) — the number of vertices in the graph and the interest value for the appropriate test. It is guaranteed that the required graph exists.

输出格式

For each of the $ t $ tests print $ 2n+p $ lines containing the description of the edges of a $ p $ -interesting graph: the $ i $ -th line must contain two space-separated integers $ a_{i},b_{i} $ ( $ 1<=a_{i},b_{i}<=n; a_{i}≠b_{i} $ ) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from $ 1 $ to $ n $ . Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.

输入输出样例

输入样例 #1

1
6 0

输出样例 #1

1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6