Toy Sum

题意翻译

### 题目描述 小克里斯非常热衷玩具积木，然而他的老师想要他好好学习去解决更多的问题，因此老师决定戏弄下克里斯。 现有$s$个积木块在克里斯的玩具箱里，每个积木块拥有$1$~$s$中的唯一编号，克里斯的老师选出一些积木保管（积木组成的集合为$X$），如果克里斯能从剩余的积木中选出一些积木组成的集合$Y$使得下面条件成立，那么老师将会还给他之前拿的积木。 条件要满足： $$\sum\limits_{x\in X}(x-1)=\sum\limits_{y\in Y}(s-y)$$ 举例来说，考虑当$s=8$的时候老师拿了$1,4,5$号的积木，那么克里斯可以挑取剩下积木中的$3,6$号作为问题的答案。也就是：$(1-1)+(4-1)+(5-1)=(8-3)+(8-6)=7$。  现在克里斯一共有$s=10^6$块积木，请你帮助他完成这个谜题。 ### 输入格式 第一行一个整数$n(1\leq n \leq 5×10^5)$，代表集合$X$里积木的个数。 第二行包括$n$个用空格隔开且互不相同的整数$x_1,x_2,...,x_n(1\leq x_i\leq 10^6)$，代表集合$X$里积木的编号。 **注意：输入输出的数据可能会很大，不要用C++的cin,cout** ### 输出格式 第一行输出一个整数$m(1\leq m\leq 10^6-n)$，代表集合$Y$中积木的个数。 第二行包括$m$个用空格隔开且互不相同的整数$y_1,y_2,...,y_m(1\leq y_i\leq 10^6)$，代表集合$Y$里积木的编号。**集合$X,Y$要保证没有交集。** **题目保证至少存在一组解，如果有多组解存在，输出任意一组。**

题目描述

Little Chris is very keen on his toy blocks. His teacher, however, wants Chris to solve more problems, so he decided to play a trick on Chris. There are exactly $ s $ blocks in Chris's set, each block has a unique number from 1 to $ s $ . Chris's teacher picks a subset of blocks $ X $ and keeps it to himself. He will give them back only if Chris can pick such a non-empty subset $ Y $ from the remaining blocks, that the equality holds: 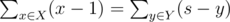 "Are you kidding me?", asks Chris.For example, consider a case where $ s=8 $ and Chris's teacher took the blocks with numbers 1, 4 and 5. One way for Chris to choose a set is to pick the blocks with numbers 3 and 6, see figure. Then the required sums would be equal: $ (1-1)+(4-1)+(5-1)=(8-3)+(8-6)=7 $ . However, now Chris has exactly $ s=10^{6} $ blocks. Given the set $ X $ of blocks his teacher chooses, help Chris to find the required set $ Y $ !

输入输出格式

输入格式

The first line of input contains a single integer $ n $ ( $ 1<=n<=5·10^{5} $ ), the number of blocks in the set $ X $ . The next line contains $ n $ distinct space-separated integers $ x_{1} $ , $ x_{2} $ , $ ... $ , $ x_{n} $ ( $ 1<=x_{i}<=10^{6} $ ), the numbers of the blocks in $ X $ . Note: since the size of the input and output could be very large, don't use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.

输出格式

In the first line of output print a single integer $ m $ ( $ 1<=m<=10^{6}-n $ ), the number of blocks in the set $ Y $ . In the next line output $ m $ distinct space-separated integers $ y_{1} $ , $ y_{2} $ , $ ... $ , $ y_{m} $ ( $ 1<=y_{i}<=10^{6} $ ), such that the required equality holds. The sets $ X $ and $ Y $ should not intersect, i.e. $ x_{i}≠y_{j} $ for all $ i $ , $ j $ ( $ 1<=i<=n $ ; $ 1<=j<=m $ ). It is guaranteed that at least one solution always exists. If there are multiple solutions, output any of them.

输入输出样例

输入样例 #1

3
1 4 5

输出样例 #1

2
999993 1000000

输入样例 #2

1
1

输出样例 #2

1
1000000