DZY Loves FFT

题意翻译

# CF444B DZY Loves FFT ## 题目描述 Dzy喜欢快速傅立叶变换，他喜欢使用它。 快速傅立叶变换是一种用于计算卷积的算法。具体地说，如果a、b和c是长度为n的序列，从0变为n-1，我们可以使用快速傅立叶变换快速计算c。 Dzy对这个公式做了一点修改。现在让事情简单点，a是从1到n的整数排列，b是一个只包含0和1的序列。给定a和b，dzy需要你的帮助来计算c。 因为他淘气，DZY提供了一种特殊的方法来获得A和B。你只需要三个整数n，d，x。获取它们之后，使用下面的代码生成A和B。 ``` //x is 64-bit variable; function getNextX() { x = (x * 37 + 10007) % 1000000007; return x; } function initAB() { for(i = 0; i < n; i = i + 1){ a[i] = i + 1; } for(i = 0; i < n; i = i + 1){ swap(a[i], a[getNextX() % (i + 1)]); } for(i = 0; i < n; i = i + 1){ if (i < d) b[i] = 1; else b[i] = 0; } for(i = 0; i < n; i = i + 1){ swap(b[i], b[getNextX() % (i + 1)]); } } ``` 操作x%y表示x除以y后的余数。函数交换（x，y）交换两个值x和y。 ## 输入格式 唯一一行输入包含三个空格分隔的整数n、d、x（1<=d<=n<=100000；0<=x<=10000000006）。因为dzy很淘气，x不能等于2777500 ## 输出格式 输出n行，第i行应包含整数c_{i-1}。

题目描述

DZY loves Fast Fourier Transformation, and he enjoys using it. Fast Fourier Transformation is an algorithm used to calculate convolution. Specifically, if $ a $ , $ b $ and $ c $ are sequences with length $ n $ , which are indexed from $ 0 $ to $ n-1 $ , and 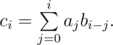We can calculate $ c $ fast using Fast Fourier Transformation. DZY made a little change on this formula. Now 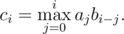To make things easier, $ a $ is a permutation of integers from $ 1 $ to $ n $ , and $ b $ is a sequence only containing $ 0 $ and $ 1 $ . Given $ a $ and $ b $ , DZY needs your help to calculate $ c $ . Because he is naughty, DZY provides a special way to get $ a $ and $ b $ . What you need is only three integers $ n $ , $ d $ , $ x $ . After getting them, use the code below to generate $ a $ and $ b $ . ``` //x is 64-bit variable; function getNextX() { x = (x * 37 + 10007) % 1000000007; return x; } function initAB() { for(i = 0; i < n; i = i + 1){ a[i] = i + 1; } for(i = 0; i < n; i = i + 1){ swap(a[i], a[getNextX() % (i + 1)]); } for(i = 0; i < n; i = i + 1){ if (i < d) b[i] = 1; else b[i] = 0; } for(i = 0; i < n; i = i + 1){ swap(b[i], b[getNextX() % (i + 1)]); } } ``` Operation x % y denotes remainder after division $ x $ by $ y $ . Function swap(x, y) swaps two values $ x $ and $ y $ .

输入输出格式

输入格式

The only line of input contains three space-separated integers $ n,d,x (1<=d<=n<=100000; 0<=x<=1000000006) $ . Because DZY is naughty, $ x $ can't be equal to $ 27777500 $ .

输出格式

Output $ n $ lines, the $ i $ -th line should contain an integer $ c_{i-1} $ .

输入输出样例

输入样例 #1

3 1 1

输出样例 #1

1
3
2

输入样例 #2

5 4 2

输出样例 #2

2
2
4
5
5

输入样例 #3

5 4 3

输出样例 #3

5
5
5
5
4

说明

In the first sample, $ a $ is $ [1\ 3\ 2] $ , $ b $ is $ [1\ 0\ 0] $ , so $ c_{0}=max(1·1)=1 $ , $ c_{1}=max(1·0,3·1)=3 $ , $ c_{2}=max(1·0,3·0,2·1)=2 $ . In the second sample, $ a $ is $ [2\ 1\ 4\ 5\ 3] $ , $ b $ is $ [1\ 1\ 1\ 0\ 1] $ . In the third sample, $ a $ is $ [5\ 2\ 1\ 4\ 3] $ , $ b $ is $ [1\ 1\ 1\ 1\ 0] $ .