DZY Loves Bridges

题意翻译

DZY是一个土豪，他有2^m座岛屿，从1至2^m编号。对于所有的不相等的u和v，岛屿u和岛屿v间建有k座不同的双向桥，k为最大的能整除|u-v|的二的整次幂。走过一座桥需要花一天时间，每座桥可以被走多次。 另外，DZY还建了一些桥连接他的家和这些岛屿。具体地，有a[i]座桥连接他的家和岛屿i。与上面不同的是，这些桥是单向的，只能从家走到岛屿。 DZY准备在岛上观光t天（不计从家走到岛屿的时间），每天他可以选择待在岛上或者走任何一座能走的桥去另外一个岛。对于每座岛，你需要求出观光结束时DZY有多少种方法出现在这个岛（任何一天的行为不同即算作不同）。 输入：第一行三个整数，依次是m，t，s。s在下文有解释。 第二行s个整数，表示a[1~s]。对于s<i<=2^m，a[i]=(101*a[i-s]+10007) mod 1051131。 输出：一行一个整数，表示每个岛屿方法数对1051131取模后的异或和。

题目描述

DZY owns $ 2^{m} $ islands near his home, numbered from $ 1 $ to $ 2^{m} $ . He loves building bridges to connect the islands. Every bridge he builds takes one day's time to walk across. DZY has a strange rule of building the bridges. For every pair of islands $ u,v (u≠v) $ , he has built $ 2^{k} $ different bridges connecting them, where 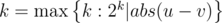 ( $ a|b $ means $ b $ is divisible by $ a $ ). These bridges are bidirectional. Also, DZY has built some bridges connecting his home with the islands. Specifically, there are $ a_{i} $ different bridges from his home to the $ i $ -th island. These are one-way bridges, so after he leaves his home he will never come back. DZY decides to go to the islands for sightseeing. At first he is at home. He chooses and walks across one of the bridges connecting with his home, and arrives at some island. After that, he will spend $ t $ day(s) on the islands. Each day, he can choose to stay and rest, or to walk to another island across the bridge. It is allowed to stay at an island for more than one day. It's also allowed to cross one bridge more than once. Suppose that right after the $ t $ -th day DZY stands at the $ i $ -th island. Let $ ans[i] $ be the number of ways for DZY to reach the $ i $ -th island after $ t $ -th day. Your task is to calculate $ ans[i] $ for each $ i $ modulo $ 1051131 $ .

输入输出格式

输入格式

To avoid huge input, we use the following way to generate the array $ a $ . You are given the first $ s $ elements of array: $ a_{1},a_{2},...,a_{s} $ . All the other elements should be calculated by formula: $ a_{i}=(101·a_{i-s}+10007) mod 1051131 $ $ (s&lt;i<=2^{m}) $ . The first line contains three integers $ m,t,s $ $ (1<=m<=25; 1<=t<=10^{18}; 1<=s<=min(2^{m},10^{5})) $ . The second line contains $ s $ integers $ a_{1},a_{2},...,a_{s} (1<=a_{i}<=10^{6}) $ .

输出格式

To avoid huge output, you only need to output xor-sum of all the answers for all $ i $ modulo $ 1051131 $ $ (1<=i<=2^{m}) $ , i.e. $ (ans[1] mod 1051131) xor (ans[2] mod 1051131) xor...\ xor (ans[n] mod 1051131) $ .

输入输出样例

输入样例 #1

2 1 4
1 1 1 2

输出样例 #1

1

输入样例 #2

3 5 6
389094 705719 547193 653800 947499 17024

输出样例 #2

556970

说明

In the first sample, $ ans=[6,7,6,6] $ . If he wants to be at island 1 after one day, he has 6 different ways: 1. home —> 1 -(stay)-> 1 2. home —> 2 —> 1 3. home —> 3 —> 1 4. home —> 3 —> 1 (note that there are two different bridges between 1 and 3) 5. home —> 4 —> 1 6. home —> 4 —> 1 (note that there are two different bridges from home to 4) In the second sample, $ (a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7},a_{8})=(389094,705719,547193,653800,947499,17024,416654,861849) $ , $ ans=[235771,712729,433182,745954,139255,935785,620229,644335] $ .