302577: CF498C. Array and Operations
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Array and Operations
题意翻译
## 题目描述 你有一个长度为n的数组a和m对数$(i_1,j_1),(i_2,j_2)...,(i_m,j_m)$ .对于每对数都满足$i_k + j_k$ 是一个奇数,且每个数都在1到n之间。 你每次操作可需要挑一对数(给定的m对里面)$ i_k,j_k$ ,然后使$a[i_k]=\frac{a[i_k]}{v},a[j_k]=\frac{a[j_k]}{v}$ ,v是一个不等于1的正整数,且$v$ 是a[i]和a[j]的公约数 问最多可以进行多少次操作 ## 输入输出格式 ### ***输入格式:*** 第一行是两个数n,m(2<=n<=100,1<=m<=100) 第二第二行n个数表示数组a,(1<=a[i]<=10^9) 接下来m行表示m对数,满足两个数的和为奇数且都在1到n之间 ### ***输出格式:*** 输出问题的答案 Translated by @doge233题目描述
You have written on a piece of paper an array of $ n $ positive integers $ a[1],a[2],...,a[n] $ and $ m $ good pairs of integers $ (i_{1},j_{1}),(i_{2},j_{2}),...,(i_{m},j_{m}) $ . Each good pair $ (i_{k},j_{k}) $ meets the following conditions: $ i_{k}+j_{k} $ is an odd number and $ 1<=i_{k}<j_{k}<=n $ . In one operation you can perform a sequence of actions: - take one of the good pairs $ (i_{k},j_{k}) $ and some integer $ v $ ( $ v>1 $ ), which divides both numbers $ a[i_{k}] $ and $ a[j_{k}] $ ; - divide both numbers by $ v $ , i. e. perform the assignments: 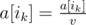 and 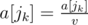. Determine the maximum number of operations you can sequentially perform on the given array. Note that one pair may be used several times in the described operations.输入输出格式
输入格式
The first line contains two space-separated integers $ n $ , $ m $ ( $ 2<=n<=100 $ , $ 1<=m<=100 $ ). The second line contains $ n $ space-separated integers $ a[1],a[2],...,a[n] $ ( $ 1<=a[i]<=10^{9} $ ) — the description of the array. The following $ m $ lines contain the description of good pairs. The $ k $ -th line contains two space-separated integers $ i_{k} $ , $ j_{k} $ ( $ 1<=i_{k}<j_{k}<=n $ , $ i_{k}+j_{k} $ is an odd number). It is guaranteed that all the good pairs are distinct.
输出格式
Output the answer for the problem.
输入输出样例
输入样例 #1
3 2
8 3 8
1 2
2 3
输出样例 #1
0
输入样例 #2
3 2
8 12 8
1 2
2 3
输出样例 #2
2