Misha and Permutations Summation

题意翻译

现在有两个$n$的排列$n$的排列是由0 1 2 ... n − 1 这$n$的数字组成的。对于一个排列$p$，$Order(p)$表示$p$是字典序第$Order(p)$小的排列（从0开始计数）。对于小于 $n!$ 的非负数$x$,$P erm(x)$表示字典序第$x$小的排列。 现在，求两个排列的和。两个排列$p$和$q$的和为$sum =Perm((Order(p) + Order(q))$$%$n!)$ 输入格式: 输入文件第一行一个数字 n，含义如题。 接下来两行，每行 n 个用空格隔开的数字，表示两个排列。 输出格式: 输出一行 n 个数字，用空格隔开，表示两个排列的和。

题目描述

Let's define the sum of two permutations $ p $ and $ q $ of numbers $ 0,1,...,(n-1) $ as permutation 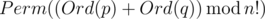, where $ Perm(x) $ is the $ x $ -th lexicographically permutation of numbers $ 0,1,...,(n-1) $ (counting from zero), and $ Ord(p) $ is the number of permutation $ p $ in the lexicographical order. For example, $ Perm(0)=(0,1,...,n-2,n-1) $ , $ Perm(n!-1)=(n-1,n-2,...,1,0) $ Misha has two permutations, $ p $ and $ q $ . Your task is to find their sum. Permutation $ a=(a_{0},a_{1},...,a_{n-1}) $ is called to be lexicographically smaller than permutation $ b=(b_{0},b_{1},...,b_{n-1}) $ , if for some $ k $ following conditions hold: $ a_{0}=b_{0},a_{1}=b_{1},...,a_{k-1}=b_{k-1},a_{k}<b_{k} $ .

输入输出格式

输入格式

The first line contains an integer $ n $ ( $ 1<=n<=200000 $ ). The second line contains $ n $ distinct integers from $ 0 $ to $ n-1 $ , separated by a space, forming permutation $ p $ . The third line contains $ n $ distinct integers from $ 0 $ to $ n-1 $ , separated by spaces, forming permutation $ q $ .

输出格式

Print $ n $ distinct integers from $ 0 $ to $ n-1 $ , forming the sum of the given permutations. Separate the numbers by spaces.

输入输出样例

输入样例 #1

2
0 1
0 1

输出样例 #1

0 1

输入样例 #2

2
0 1
1 0

输出样例 #2

1 0

输入样例 #3

3
1 2 0
2 1 0

输出样例 #3

1 0 2

说明

Permutations of numbers from 0 to 1 in the lexicographical order: $ (0,1),(1,0) $ . In the first sample $ Ord(p)=0 $ and $ Ord(q)=0 $ , so the answer is . In the second sample $ Ord(p)=0 $ and $ Ord(q)=1 $ , so the answer is . Permutations of numbers from 0 to 2 in the lexicographical order: $ (0,1,2),(0,2,1),(1,0,2),(1,2,0),(2,0,1),(2,1,0) $ . In the third sample $ Ord(p)=3 $ and $ Ord(q)=5 $ , so the answer is .