302605: CF505D. Mr. Kitayuta's Technology
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Mr. Kitayuta's Technology
题意翻译
## 题目描述 Shuseki Kingdom在创新和技术方面是世界领先的国家。在Shuseki Kingdom中有编号1到n的n个城市。 Kitayuta先生的研究使Shuseki Kingdom会在两个城市之间建造传送管道。连接两个城市的传送管道是单向的,即从城市x到城市y的传送管道不能用来从城市y前往城市x。由于每个城市内的交通极为发达,因此如果从城市x到城市y的传送管道和从城市y到城市z的传送管道都已建造好,人们就可以直接从城市x前往城市z。 Kitayuta先生同时也是一个政客。他认为有m对“重要城市对”(ai,bi) ( 1<=i<=m )之间的交通很重要。他计划建造传送管道时,要使得对于每对“重要城市对”(ai,bi),都可以通过使用一个或多个传送管道,从城市ai前往城市bi。请你计算出,最少需要建造几条传送管道,才能满足Kitayuta先生的需求。到目前为止,还没有建造任何传送管道,城市之间也没有任何其他有效的交通工具。 ## 输入输出格式 #### 输入格式: 输入共m+1行 第一行,两个以空格分隔的整数n和m(2 <= n<= 10 ^ 5,1 <= m<= 10 ^ 5),分别表示Shuseki王国的城市数量和重要城市对的数量。 接下来的m行中,每行有两个数字ai和bi,( 1<=ai,bi<=n,ai≠bi ),表示从城市ai必须能通过一个或多个传送管道到达城市bi(但不必保证能从城市bi前往城市ai)。保证每对重要城市对都是不同的。 #### 输出格式: 输出共1行,一个整数,表示能使得Kitayuta先生的需求满足的传送管道的数量的最小值。 ## 说明 对于第一个样例,构建管道的最佳方法之一如下图所示: 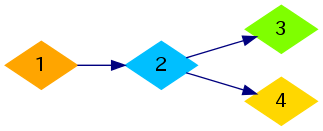 对于第二个样例,构建管道的最佳方法之一如下图所示: 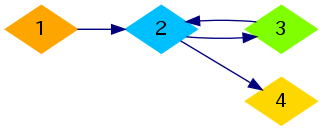题目描述
Shuseki Kingdom is the world's leading nation for innovation and technology. There are $ n $ cities in the kingdom, numbered from $ 1 $ to $ n $ . Thanks to Mr. Kitayuta's research, it has finally become possible to construct teleportation pipes between two cities. A teleportation pipe will connect two cities unidirectionally, that is, a teleportation pipe from city $ x $ to city $ y $ cannot be used to travel from city $ y $ to city $ x $ . The transportation within each city is extremely developed, therefore if a pipe from city $ x $ to city $ y $ and a pipe from city $ y $ to city $ z $ are both constructed, people will be able to travel from city $ x $ to city $ z $ instantly. Mr. Kitayuta is also involved in national politics. He considers that the transportation between the $ m $ pairs of city $ (a_{i},b_{i}) $ ( $ 1<=i<=m $ ) is important. He is planning to construct teleportation pipes so that for each important pair $ (a_{i},b_{i}) $ , it will be possible to travel from city $ a_{i} $ to city $ b_{i} $ by using one or more teleportation pipes (but not necessarily from city $ b_{i} $ to city $ a_{i} $ ). Find the minimum number of teleportation pipes that need to be constructed. So far, no teleportation pipe has been constructed, and there is no other effective transportation between cities.输入输出格式
输入格式
The first line contains two space-separated integers $ n $ and $ m $ ( $ 2<=n<=10^{5},1<=m<=10^{5} $ ), denoting the number of the cities in Shuseki Kingdom and the number of the important pairs, respectively. The following $ m $ lines describe the important pairs. The $ i $ -th of them ( $ 1<=i<=m $ ) contains two space-separated integers $ a_{i} $ and $ b_{i} $ ( $ 1<=a_{i},b_{i}<=n,a_{i}≠b_{i} $ ), denoting that it must be possible to travel from city $ a_{i} $ to city $ b_{i} $ by using one or more teleportation pipes (but not necessarily from city $ b_{i} $ to city $ a_{i} $ ). It is guaranteed that all pairs $ (a_{i},b_{i}) $ are distinct.
输出格式
Print the minimum required number of teleportation pipes to fulfill Mr. Kitayuta's purpose.
输入输出样例
输入样例 #1
4 5
1 2
1 3
1 4
2 3
2 4
输出样例 #1
3
输入样例 #2
4 6
1 2
1 4
2 3
2 4
3 2
3 4
输出样例 #2
4