Fox And Dinner

题意翻译

# 题目描述 小狐狸Ciel参加了一个派对，加上他自己这个派对里总共有$n$只狐狸，每只狐狸有一个年龄$a_i$。 它们想要在几张圆桌旁吃晚饭，你需要帮忙分配座位，使得满足以下要求： 1. 每只狐狸都在其中 2. 每张桌子边至少有3只狐狸 3. 任意两只相邻的狐狸的年龄之和为质数（圆桌上每只狐狸都有2只相邻的狐狸） # 输入格式 第一行一个正整数$n(3 \le n \le 200)$，表示狐狸个数。 第二行$n$个正整数$a_i(2 \le a_i \le 10^4)$，表示每只狐狸的年龄。 # 输出格式 如果不可能有满足要求的分配方式，输出"Impossible"。 否则，第一行输出一个正整数$m$表示桌数。 然后输出$m$行，每行先一个整数$k$表示这桌的狐狸数，然后$k$个正整数表示这桌的狐狸编号（按照顺序输出，但从哪个编号开始没有关系）。 如果有多组解，输出任意一组。 # 样例解释 样例一：只需要一桌，顺序为$3-8-9-4$，相邻的和分别是$11,17,13,7$，全都是质数。 样例二：不可能，$2+2=4$不是质数。

题目描述

Fox Ciel is participating in a party in Prime Kingdom. There are $ n $ foxes there (include Fox Ciel). The i-th fox is $ a_{i} $ years old. They will have dinner around some round tables. You want to distribute foxes such that: 1. Each fox is sitting at some table. 2. Each table has at least 3 foxes sitting around it. 3. The sum of ages of any two adjacent foxes around each table should be a prime number. If $ k $ foxes $ f_{1} $ , $ f_{2} $ , ..., $ f_{k} $ are sitting around table in clockwise order, then for $ 1<=i<=k-1 $ : $ f_{i} $ and $ f_{i+1} $ are adjacent, and $ f_{1} $ and $ f_{k} $ are also adjacent. If it is possible to distribute the foxes in the desired manner, find out a way to do that.

输入输出格式

输入格式

The first line contains single integer $ n $ ( $ 3<=n<=200 $ ): the number of foxes in this party. The second line contains $ n $ integers $ a_{i} $ ( $ 2<=a_{i}<=10^{4} $ ).

输出格式

If it is impossible to do this, output "Impossible". Otherwise, in the first line output an integer $ m $ (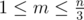): the number of tables. Then output $ m $ lines, each line should start with an integer $ k $ -=– the number of foxes around that table, and then $ k $ numbers — indices of fox sitting around that table in clockwise order. If there are several possible arrangements, output any of them.

输入输出样例

输入样例 #1

4
3 4 8 9

输出样例 #1

1
4 1 2 4 3

输入样例 #2

5
2 2 2 2 2

输出样例 #2

Impossible

输入样例 #3

12
2 3 4 5 6 7 8 9 10 11 12 13

输出样例 #3

1
12 1 2 3 6 5 12 9 8 7 10 11 4

输入样例 #4

24
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

输出样例 #4

3
6 1 2 3 6 5 4
10 7 8 9 12 15 14 13 16 11 10
8 17 18 23 22 19 20 21 24

说明

In example 1, they can sit around one table, their ages are: 3-8-9-4, adjacent sums are: 11, 17, 13 and 7, all those integers are primes. In example 2, it is not possible: the sum of 2+2 = 4 is not a prime number.

题意翻译

# 题目描述 小狐狸Ciel参加了一个派对，加上他自己这个派对里总共有$n$只狐狸，每只狐狸有一个年龄$a_i$。 它们想要在几张圆桌旁吃晚饭，你需要帮忙分配座位，使得满足以下要求： 1. 每只狐狸都在其中 2. 每张桌子边至少有3只狐狸 3. 任意两只相邻的狐狸的年龄之和为质数（圆桌上每只狐狸都有2只相邻的狐狸） # 输入格式 第一行一个正整数$n(3 \le n \le 200)$，表示狐狸个数。 第二行$n$个正整数$a_i(2 \le a_i \le 10^4)$，表示每只狐狸的年龄。 # 输出格式 如果不可能有满足要求的分配方式，输出"Impossible"。 否则，第一行输出一个正整数$m$表示桌数。 然后输出$m$行，每行先一个整数$k$表示这桌的狐狸数，然后$k$个正整数表示这桌的狐狸编号（按照顺序输出，但从哪个编号开始没有关系）。 如果有多组解，输出任意一组。 # 样例解释 样例一：只需要一桌，顺序为$3-8-9-4$，相邻的和分别是$11,17,13,7$，全都是质数。 样例二：不可能，$2+2=4$不是质数。