Playing on Graph

题意翻译

Vova和Marina喜欢互相提供谜题。今天，Marina提供Vova来应对以下任务。 Vova有一个无向图，由n个顶点和m边组成，没有自环和重边。让我们定义两个不能通过一条边联通的点a和b的收缩操作，它们不是由边连接的。此操作的结果如下： 1.顶点a和b被删除 2新的顶点x被添加到图形中，并且连接x与和a,b都直接相连的点（具体地说，如果点p与a和b都连接，然后从x向p连一条边）。 因此，多次收缩的结果是无向图，它不包含环和重边，并且它包含（n-1）个顶点。 Vova必须执行任意次数的收缩，才能将给定的图形转换为最大长度的链。长度为k（k> = 0）的链是一个连通图，其顶点可以用从1到k+1的整数编号，这样就可以得到边（i，i+1）（1<=i<=k）且图中只有这些边。特别的，由一个点组成的图是长度为0的链。由于收缩而形成的点被允许用于之后收缩操作。 图为红色标记的两个顶点的收缩。帮助Vova完成女友的任务。找到可以获得的链的最大长度，或者确定无法获得链

题目描述

Vova and Marina love offering puzzles to each other. Today Marina offered Vova to cope with the following task. Vova has a non-directed graph consisting of $ n $ vertices and $ m $ edges without loops and multiple edges. Let's define the operation of contraction two vertices $ a $ and $ b $ that are not connected by an edge. As a result of this operation vertices $ a $ and $ b $ are deleted and instead of them a new vertex $ x $ is added into the graph, and also edges are drawn from it to all vertices that were connected with $ a $ or with $ b $ (specifically, if the vertex was connected with both $ a $ and $ b $ , then also exactly one edge is added from $ x $ to it). Thus, as a result of contraction again a non-directed graph is formed, it contains no loops nor multiple edges, and it contains $ (n-1) $ vertices. Vova must perform the contraction an arbitrary number of times to transform the given graph into a chain of the maximum length. A chain of length $ k $ ( $ k>=0 $ ) is a connected graph whose vertices can be numbered with integers from $ 1 $ to $ k+1 $ so that the edges of the graph connect all pairs of vertices $ (i,i+1) $ ( $ 1<=i<=k $ ) and only them. Specifically, the graph that consists of one vertex is a chain of length $ 0 $ . The vertices that are formed as a result of the contraction are allowed to be used in the following operations of contraction. 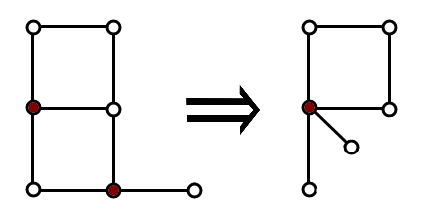The picture illustrates the contraction of two vertices marked by red.Help Vova cope with his girlfriend's task. Find the maximum length of the chain that can be obtained from the resulting graph or else determine that it is impossible to obtain the chain.

输入输出格式

输入格式

The first line contains two integers $ n,m $ ( $ 1<=n<=1000 $ , $ 0<=m<=100000 $ ) — the number of vertices and the number of edges in the original graph. Next $ m $ lines contain the descriptions of edges in the format $ a_{i},b_{i} $ ( $ 1<=a_{i},b_{i}<=n $ , $ a_{i}≠b_{i} $ ), which means that there is an edge between vertices $ a_{i} $ and $ b_{i} $ . It is guaranteed that there is at most one edge between each pair of vertexes.

输出格式

If it is impossible to obtain a chain from the given graph, print $ -1 $ . Otherwise, print the maximum possible number of edges in the resulting chain.

输入输出样例

输入样例 #1

5 4
1 2
2 3
3 4
3 5

输出样例 #1

3

输入样例 #2

4 6
1 2
2 3
1 3
3 4
2 4
1 4

输出样例 #2

-1

输入样例 #3

4 2
1 3
2 4

输出样例 #3

2

说明

In the first sample test you can contract vertices $ 4 $ and $ 5 $ and obtain a chain of length $ 3 $ . In the second sample test it is initially impossible to contract any pair of vertexes, so it is impossible to achieve the desired result. In the third sample test you can contract vertices $ 1 $ and $ 2 $ and obtain a chain of length $ 2 $ .