Nudist Beach

题意翻译

有n座城市由m条双向道路连接。现在所有的城市都已经被敌人攻陷了，敌人还在其中k座城市中建起了堡垒，这些城市无法被攻克；我们需要从敌人手中夺回一些城市，使得所有夺回的城市都尽可能安全，即最小的安全度尽可能大。定义一座城市的安全度为它的所有邻居中由我方控制的城市数量除以它的所有邻居数量。 n，m <= 10^5

题目描述

Nudist Beach is planning a military operation to attack the Life Fibers. In this operation, they will attack and capture several cities which are currently under the control of the Life Fibers. There are $ n $ cities, labeled from 1 to $ n $ , and $ m $ bidirectional roads between them. Currently, there are Life Fibers in every city. In addition, there are $ k $ cities that are fortresses of the Life Fibers that cannot be captured under any circumstances. So, the Nudist Beach can capture an arbitrary non-empty subset of cities with no fortresses. After the operation, Nudist Beach will have to defend the captured cities from counterattack. If they capture a city and it is connected to many Life Fiber controlled cities, it will be easily defeated. So, Nudist Beach would like to capture a set of cities such that for each captured city the ratio of Nudist Beach controlled neighbors among all neighbors of that city is as high as possible. More formally, they would like to capture a non-empty set of cities $ S $ with no fortresses of Life Fibers. The strength of a city 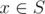 is defined as (number of neighbors of $ x $ in $ S $ ) / (total number of neighbors of $ x $ ). Here, two cities are called neighbors if they are connnected with a road. The goal is to maximize the strength of the weakest city in $ S $ . Given a description of the graph, and the cities with fortresses, find a non-empty subset that maximizes the strength of the weakest city.

输入输出格式

输入格式

The first line of input contains three integers $ n,m,k $ ( $ 2<=n<=100000 $ , $ 1<=m<=100000 $ , $ 1<=k<=n-1 $ ). The second line of input contains $ k $ integers, representing the cities with fortresses. These cities will all be distinct. The next $ m $ lines contain the roads. The $ i $ -th of these lines will have 2 integers $ a_{i},b_{i} $ ( $ 1<=a_{i},b_{i}<=n $ , $ a_{i}≠b_{i} $ ). Every city will have at least one road adjacent to it. There is no more than one road between each pair of the cities.

输出格式

The first line should contain an integer $ r $ , denoting the size of an optimum set ( $ 1<=r<=n-k $ ). The second line should contain $ r $ integers, denoting the cities in the set. Cities may follow in an arbitrary order. This line should not contain any of the cities with fortresses. If there are multiple possible answers, print any of them.

输入输出样例

输入样例 #1

9 8 4
3 9 6 8
1 2
1 3
1 4
1 5
2 6
2 7
2 8
2 9

输出样例 #1

3
1 4 5

输入样例 #2

10 8 2
2 9
1 3
2 9
4 5
5 6
6 7
7 8
8 10
10 4

输出样例 #2

8
1 5 4 8 10 6 3 7

说明

The first example case achieves a strength of 1/2. No other subset is strictly better. The second example case achieves a strength of 1. Note that the subset doesn't necessarily have to be connected.