Edo and Magnets

题意翻译

在一个平面直角坐标系中有 $n$ 个矩形。设一个矩形的左下角坐标为 $(x_1,y_1)$ ， 右上角坐标为 $(x_2,y_2)$ ，定义其中心为$(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$ 。 对于给定的 $n$ 个矩形，你最多可以删除 $k$ 个矩形（可以不删），使得包含全部剩余矩形的最小矩形的面积最小。定义矩形 $a$ 包含矩形 $b$ 当且仅当矩形 $b$ 的中心在矩形 $a$ 的边缘或内部。 注意，虽然输入中每个矩形的顶点坐标一定为整数，但是其中心坐标可能不是整数，这时不需要取整，直接使用小数计算。只包含一个点的矩形大小为 $1\times1$ 。

题目描述

Edo has got a collection of $ n $ refrigerator magnets! He decided to buy a refrigerator and hang the magnets on the door. The shop can make the refrigerator with any size of the door that meets the following restrictions: the refrigerator door must be rectangle, and both the length and the width of the door must be positive integers. Edo figured out how he wants to place the magnets on the refrigerator. He introduced a system of coordinates on the plane, where each magnet is represented as a rectangle with sides parallel to the coordinate axes. Now he wants to remove no more than $ k $ magnets (he may choose to keep all of them) and attach all remaining magnets to the refrigerator door, and the area of ​​the door should be as small as possible. A magnet is considered to be attached to the refrigerator door if its center lies on the door or on its boundary. The relative positions of all the remaining magnets must correspond to the plan. Let us explain the last two sentences. Let's suppose we want to hang two magnets on the refrigerator. If the magnet in the plan has coordinates of the lower left corner ( $ x_{1} $ , $ y_{1} $ ) and the upper right corner ( $ x_{2} $ , $ y_{2} $ ), then its center is located at (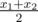, ) (may not be integers). By saying the relative position should correspond to the plan we mean that the only available operation is translation, i.e. the vector connecting the centers of two magnets in the original plan, must be equal to the vector connecting the centers of these two magnets on the refrigerator. The sides of the refrigerator door must also be parallel to coordinate axes.

输入输出格式

输入格式

The first line contains two integers $ n $ and $ k $ ( $ 1<=n<=100000 $ , $ 0<=k<=min(10,n-1) $ ) — the number of magnets that Edo has and the maximum number of magnets Edo may not place on the refrigerator. Next $ n $ lines describe the initial plan of placing magnets. Each line contains four integers $ x_{1},y_{1},x_{2},y_{2} $ ( $ 1<=x_{1}&lt;x_{2}<=10^{9} $ , $ 1<=y_{1}&lt;y_{2}<=10^{9} $ ) — the coordinates of the lower left and upper right corners of the current magnet. The magnets can partially overlap or even fully coincide.

输出格式

Print a single integer — the minimum area of the door of refrigerator, which can be used to place at least $ n-k $ magnets, preserving the relative positions.

输入输出样例

输入样例 #1

3 1
1 1 2 2
2 2 3 3
3 3 4 4

输出样例 #1

1

输入样例 #2

4 1
1 1 2 2
1 9 2 10
9 9 10 10
9 1 10 2

输出样例 #2

64

输入样例 #3

3 0
1 1 2 2
1 1 1000000000 1000000000
1 3 8 12

输出样例 #3

249999999000000001

说明

In the first test sample it is optimal to remove either the first or the third magnet. If we remove the first magnet, the centers of two others will lie at points (2.5, 2.5) and (3.5, 3.5). Thus, it is enough to buy a fridge with door width 1 and door height 1, the area of the door also equals one, correspondingly. In the second test sample it doesn't matter which magnet to remove, the answer will not change — we need a fridge with door width 8 and door height 8. In the third sample you cannot remove anything as $ k=0 $ .