Lipshitz Sequence

题意翻译

**【题目翻译】** 对于一个序列 $v_{1...n}$，当 $1\leq x<y\leq n$ 且 $x,y$ 均为整数时，同样满足$|v_x-v_y|\leq K\times |x-y|$，则称 $K$ 的最小整数值为序列 $v$ 的 Lipschitz 常数。现在给你一个长度为 $n$ 的序列 $v$ 并给出 $q$ 个询问，对于每对询问 $[l,r]$， 你需要求出 $v_{l...r}$ 的所有连续子序列（子段）$v_{x,y}(l\leq x<y\leq r)$ 的 Lipschitz 常数之和。 **【输入格式】** 第一行两个整数 $n$ 和 $q$，分别表示序列的长度以及询问的个数。 第二行 $n$ 个数，表示序列 $v,(0\leq v_i\leq 10^8)$。接下来 $q$ 行，每行两个数 $l$ 和 $r$，表示询问的区间为 $[l,r]$。 **【输出格式】** 对于每个询问，输出一行一个数，即 $v_{l,r}$ 的所有连续子序列（子段）的 Lipschitz 常数之和。

题目描述

A function 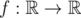 is called Lipschitz continuous if there is a real constant $ K $ such that the inequality $ |f(x)-f(y)|<=K·|x-y| $ holds for all 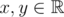. We'll deal with a more... discrete version of this term. For an array 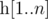, we define it's Lipschitz constant 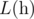 as follows: - if $ n&l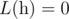t;2 $ ,  - if $ n>=2 $ , 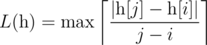 over all $ 1<=i&lt;j<=n $ In other words, 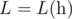 is the smallest non-negative integer such that $ |h[i]-h[j]|<=L·|i-j| $ holds for all $ 1<=i,j<=n $ . You are given an array  of size $ n $ and $ q $ queries of the form $ [l,r] $ . For each query, consider the subarray 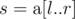; determine the sum of Lipschitz constants of all subarrays of .

输入输出格式

输入格式

The first line of the input contains two space-separated integers $ n $ and $ q $ ( $ 2<=n<=100000 $ and $ 1<=q<=100 $ ) — the number of elements in array  and the number of queries respectively. The second line contains $ n $ space-separated integers 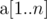 (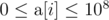). The following $ q $ lines describe queries. The $ i $ -th of those lines contains two space-separated integers $ l_{i} $ and $ r_{i} $ ( $ 1<=l_{i}&lt;r_{i}<=n $ ).

输出格式

Print the answers to all queries in the order in which they are given in the input. For the $ i $ -th query, print one line containing a single integer — the sum of Lipschitz constants of all subarrays of .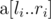

输入输出样例

输入样例 #1

10 4
1 5 2 9 1 3 4 2 1 7
2 4
3 8
7 10
1 9

输出样例 #1

17
82
23
210

输入样例 #2

7 6
5 7 7 4 6 6 2
1 2
2 3
2 6
1 7
4 7
3 5

输出样例 #2

2
0
22
59
16
8

说明

In the first query of the first sample, the Lipschitz constants of subarrays of  with length at least $ 2 $ are: -  -  -  The answer to the query is their sum.

题意翻译

**【题目翻译】** 对于一个序列 $v_{1...n}$，当 $1\leq x<y\leq n$ 且 $x,y$ 均为整数时，同样满足$|v_x-v_y|\leq K\times |x-y|$，则称 $K$ 的最小整数值为序列 $v$ 的 Lipschitz 常数。现在给你一个长度为 $n$ 的序列 $v$ 并给出 $q$ 个询问，对于每对询问 $[l,r]$， 你需要求出 $v_{l...r}$ 的所有连续子序列（子段）$v_{x,y}(l\leq x<y\leq r)$ 的 Lipschitz 常数之和。 **【输入格式】** 第一行两个整数 $n$ 和 $q$，分别表示序列的长度以及询问的个数。 第二行 $n$ 个数，表示序列 $v,(0\leq v_i\leq 10^8)$。接下来 $q$ 行，每行两个数 $l$ 和 $r$，表示询问的区间为 $[l,r]$。 **【输出格式】** 对于每个询问，输出一行一个数，即 $v_{l,r}$ 的所有连续子序列（子段）的 Lipschitz 常数之和。