Ruminations on Ruminants

题意翻译

## 题目描述 有 $n$ 条直线，两两不平行，任意 $3$ 条直线不经过同一个点。求三条直线围成的三角形的外接圆过原点的方案数。 ## 输入输出格式 ### 输入格式： 输入的第一行有一个整数$n$（$3\leq n\leq 2000$） 第二行到第 $n+1$ 行有三个整数 $a_i,b_i,c_i$（$a_i,b_i,c_i\leq 10000$）表示第 $i$ 条直线的方程为$a_ix+b_iy=c_i$ ### 输出格式： 输出无序整数对$(i,j,k)$的个数使这三条直线围成的三角形的外接圆过原点。

题目描述

Kevin Sun is ruminating on the origin of cows while standing at the origin of the Cartesian plane. He notices $ n $ lines 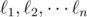 on the plane, each representable by an equation of the form $ ax+by=c $ . He also observes that no two lines are parallel and that no three lines pass through the same point. For each triple $ (i,j,k) $ such that $ 1<=i&lt;j&lt;k<=n $ , Kevin considers the triangle formed by the three lines 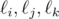 . He calls a triangle original if the circumcircle of that triangle passes through the origin. Since Kevin believes that the circles of bovine life are tied directly to such triangles, he wants to know the number of original triangles formed by unordered triples of distinct lines. Recall that the circumcircle of a triangle is the circle which passes through all the vertices of that triangle.

输入输出格式

输入格式

The first line of the input contains a single integer $ n $ ( $ 3<=n<=2000 $ ), the number of lines. The next $ n $ lines describe lines 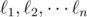. The $ i $ -th of these lines contains three space-separated integers $ a_{i},b_{i},c_{i} $ ( $ |a_{i}|,|b_{i}|,|c_{i}|<=10000,a_{i}^{2}+b_{i}^{2}&gt;0 $ ), representing the equation $ a_{i}x+b_{i}y=c_{i} $ of line .

输出格式

Print a single integer, the number of triples $ (i,j,k) $ with $ i&lt;j&lt;k $ such that lines 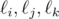 form an original triangle.

输入输出样例

输入样例 #1

4
1 0 0
0 1 0
1 1 -1
1 -1 2

输出样例 #1

2

输入样例 #2

3
0 1 1
1 1 2
1 -1 -2

输出样例 #2

1

说明

Note that in the first sample, some of the lines pass through the origin. In the second sample, there is exactly one triple of lines: $ y=1,x+y=2,x-y=-2. $ The triangle they form has vertices $ (0,2),(1,1),(-1,1) $ . The circumcircle of this triangle has equation $ x^{2}+(y-1)^{2}=1 $ . This indeed passes through $ (0,0). $