Lazy Student

题意翻译

### 题目描述 输入一个图，输出其最小生成树。 ### 输入格式 第一行包含两个整数 $n$ 和 $m$，即图中的顶点数和边数。 接下来的m行为图的一条边，由两个整数 $a_j$ 和 $b_j$ 组成 $a_j$ 是此边的权值，如果此边包含在最小生成树中，则 $b_j$ 为 1，否则为 0。 保证输入 第 $n−1$ 行的 $b_j$ 等于 1，第 $m-n+1$ 行的 $b_j$ 等于 0。 ### 输出格式 如果最小生成树不存在，请输出 -1。 否则输出 $m$ 行。在第 $j$ 行打印一对顶点 $(u_j，v_j)$，它们应该由第 $j$ 条边连接。边的输入与输出顺序相同。 必须是连通图，不包含循环或多条边，且其$b_j=1$ 的边必须为最小生成树。 如果有多种解，请输出任意一个解。

题目描述

Student Vladislav came to his programming exam completely unprepared as usual. He got a question about some strange algorithm on a graph — something that will definitely never be useful in real life. He asked a girl sitting next to him to lend him some cheat papers for this questions and found there the following definition: The minimum spanning tree $ T $ of graph $ G $ is such a tree that it contains all the vertices of the original graph $ G $ , and the sum of the weights of its edges is the minimum possible among all such trees. Vladislav drew a graph with $ n $ vertices and $ m $ edges containing no loops and multiple edges. He found one of its minimum spanning trees and then wrote for each edge its weight and whether it is included in the found tree or not. Unfortunately, the piece of paper where the graph was painted is gone and the teacher is getting very angry and demands to see the original graph. Help Vladislav come up with a graph so that the information about the minimum spanning tree remains correct.

输入输出格式

输入格式

The first line of the input contains two integers $ n $ and $ m $ (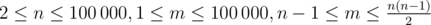) — the number of vertices and the number of edges in the graph. Each of the next $ m $ lines describes an edge of the graph and consists of two integers $ a_{j} $ and $ b_{j} $ ( $ 1<=a_{j}<=10^{9},b_{j}={0,1} $ ). The first of these numbers is the weight of the edge and the second number is equal to $ 1 $ if this edge was included in the minimum spanning tree found by Vladislav, or $ 0 $ if it was not. It is guaranteed that exactly $ n-1 $ number $ {b_{j}} $ are equal to one and exactly $ m-n+1 $ of them are equal to zero.

输出格式

If Vladislav has made a mistake and such graph doesn't exist, print $ -1 $ . Otherwise print $ m $ lines. On the $ j $ -th line print a pair of vertices $ (u_{j},v_{j}) $ ( $ 1<=u_{j},v_{j}<=n,u_{j}≠v_{j} $ ), that should be connected by the $ j $ -th edge. The edges are numbered in the same order as in the input. The graph, determined by these edges, must be connected, contain no loops or multiple edges and its edges with $ b_{j}=1 $ must define the minimum spanning tree. In case there are multiple possible solutions, print any of them.

输入输出样例

输入样例 #1

4 5
2 1
3 1
4 0
1 1
5 0

输出样例 #1

2 4
1 4
3 4
3 1
3 2

输入样例 #2

3 3
1 0
2 1
3 1

输出样例 #2

-1

题意翻译

### 题目描述 输入一个图，输出其最小生成树。 ### 输入格式 第一行包含两个整数 $n$ 和 $m$，即图中的顶点数和边数。 接下来的m行为图的一条边，由两个整数 $a_j$ 和 $b_j$ 组成 $a_j$ 是此边的权值，如果此边包含在最小生成树中，则 $b_j$ 为 1，否则为 0。 保证输入 第 $n−1$ 行的 $b_j$ 等于 1，第 $m-n+1$ 行的 $b_j$ 等于 0。 ### 输出格式 如果最小生成树不存在，请输出 -1。 否则输出 $m$ 行。在第 $j$ 行打印一对顶点 $(u_j，v_j)$，它们应该由第 $j$ 条边连接。边的输入与输出顺序相同。 必须是连通图，不包含循环或多条边，且其$b_j=1$ 的边必须为最小生成树。 如果有多种解，请输出任意一个解。