Hamiltonian Spanning Tree

题意翻译

###### 题目描述： n 个城市之间形成了一个有n*(n-1)/2条边的完全无向图。走每条边需要y秒。 给定该图的一个n-1条边的生成树，走树上的每一条边只需要x秒（不过注意x不一定小于y）。 你希望从任意一个点开始，经过每个点恰好一次，在任意一个点结束的路径的长度所花时间最少。求最少时间。 ###### 输入格式： 第一行包含三个整数 n,x,y 接下来 n−1行每行包含两个整数a和b，表示生成树上a与 b之间有一条边。保证这些边形成一棵生成树。 ###### 输出格式： 输出一个整数，表示环游城市最小时间。

题目描述

A group of $ n $ cities is connected by a network of roads. There is an undirected road between every pair of cities, so there are 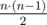 roads in total. It takes exactly $ y $ seconds to traverse any single road. A spanning tree is a set of roads containing exactly $ n-1 $ roads such that it's possible to travel between any two cities using only these roads. Some spanning tree of the initial network was chosen. For every road in this tree the time one needs to traverse this road was changed from $ y $ to $ x $ seconds. Note that it's not guaranteed that $ x $ is smaller than $ y $ . You would like to travel through all the cities using the shortest path possible. Given $ n $ , $ x $ , $ y $ and a description of the spanning tree that was chosen, find the cost of the shortest path that starts in any city, ends in any city and visits all cities exactly once.

输入输出格式

输入格式

The first line of the input contains three integers $ n $ , $ x $ and $ y $ ( $ 2<=n<=200000,1<=x,y<=10^{9} $ ). Each of the next $ n-1 $ lines contains a description of a road in the spanning tree. The $ i $ -th of these lines contains two integers $ u_{i} $ and $ v_{i} $ ( $ 1<=u_{i},v_{i}<=n $ ) — indices of the cities connected by the $ i $ -th road. It is guaranteed that these roads form a spanning tree.

输出格式

Print a single integer — the minimum number of seconds one needs to spend in order to visit all the cities exactly once.

输入输出样例

输入样例 #1

5 2 3
1 2
1 3
3 4
5 3

输出样例 #1

9

输入样例 #2

5 3 2
1 2
1 3
3 4
5 3

输出样例 #2

8

说明

In the first sample, roads of the spanning tree have cost $ 2 $ , while other roads have cost $ 3 $ . One example of an optimal path is . In the second sample, we have the same spanning tree, but roads in the spanning tree cost 3, while other roads cost 2. One example of an optimal path is .

题意翻译

###### 题目描述： n 个城市之间形成了一个有n*(n-1)/2条边的完全无向图。走每条边需要y秒。 给定该图的一个n-1条边的生成树，走树上的每一条边只需要x秒（不过注意x不一定小于y）。 你希望从任意一个点开始，经过每个点恰好一次，在任意一个点结束的路径的长度所花时间最少。求最少时间。 ###### 输入格式： 第一行包含三个整数 n,x,y 接下来 n−1行每行包含两个整数a和b，表示生成树上a与 b之间有一条边。保证这些边形成一棵生成树。 ###### 输出格式： 输出一个整数，表示环游城市最小时间。