Raffles

题意翻译

- 有 $n$ 个奖池，第 $i$ 个奖池的奖金是 $p_i$，已经有 $l_i$ 张彩票押在上面。 - 现在你有 $t$ 张彩票，你需要将你的彩票分配到这些奖池中，并且保证你在每个奖池中押的彩票数**不能超过该奖池原有的彩票数**。 - 若你在第 $i$ 个奖池中押了 $t_i$ 张彩票，则你中奖的概率为 $\frac{t_i}{t_i + l_i}$，若你中奖，你可以获得这个奖池的全部奖金 $p_i$。 - 一共有 $q$ 次事件，每次事件会使某个 $l_i$ 加 $1$ 或减 $1$。 - 你需要在每个事件后求出在最佳方案下你获得的奖金总数的最大期望值。 - $n,t,q \le 2 \times 10^5$，$p_i,l_i \le 10^3$，答案精度误差 $\le 10^{-6}$。

题目描述

Johnny is at a carnival which has $ n $ raffles. Raffle $ i $ has a prize with value $ p_{i} $ . Each participant can put tickets in whichever raffles they choose (they may have more than one ticket in a single raffle). At the end of the carnival, one ticket is selected at random from each raffle, and the owner of the ticket wins the associated prize. A single person can win multiple prizes from different raffles. However, county rules prevent any one participant from owning more than half the tickets in a single raffle, i.e. putting more tickets in the raffle than all the other participants combined. To help combat this (and possibly win some prizes), the organizers started by placing a single ticket in each raffle, which they will never remove. Johnny bought $ t $ tickets and is wondering where to place them. Currently, there are a total of $ l_{i} $ tickets in the $ i $ -th raffle. He watches as other participants place tickets and modify their decisions and, at every moment in time, wants to know how much he can possibly earn. Find the maximum possible expected value of Johnny's winnings at each moment if he distributes his tickets optimally. Johnny may redistribute all of his tickets arbitrarily between each update, but he may not place more than $ t $ tickets total or have more tickets in a single raffle than all other participants combined.

输入输出格式

输入格式

The first line contains two integers $ n $ , $ t $ , and $ q $ ( $ 1<=n,t,q<=200\ 000 $ ) — the number of raffles, the number of tickets Johnny has, and the total number of updates, respectively. The second line contains $ n $ space-separated integers $ p_{i} $ ( $ 1<=p_{i}<=1000 $ ) — the value of the $ i $ -th prize. The third line contains $ n $ space-separated integers $ l_{i} $ ( $ 1<=l_{i}<=1000 $ ) — the number of tickets initially in the $ i $ -th raffle. The last $ q $ lines contain the descriptions of the updates. Each description contains two integers $ t_{k} $ , $ r_{k} $ ( $ 1<=t_{k}<=2 $ , $ 1<=r_{k}<=n $ ) — the type of the update and the raffle number. An update of type $ 1 $ represents another participant adding a ticket to raffle $ r_{k} $ . An update of type $ 2 $ represents another participant removing a ticket from raffle $ r_{k} $ . It is guaranteed that, after each update, each raffle has at least $ 1 $ ticket (not including Johnny's) in it.

输出格式

Print $ q $ lines, each containing a single real number — the maximum expected value of Johnny's winnings after the $ k $ -th update. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ . Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct, if .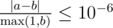

输入输出样例

输入样例 #1

2 1 3
4 5
1 2
1 1
1 2
2 1

输出样例 #1

1.666666667
1.333333333
2.000000000

输入样例 #2

3 20 5
6 8 10
6 6 6
1 1
1 2
1 3
2 3
2 3

输出样例 #2

12.000000000
12.000000000
11.769230769
12.000000000
12.000000000

说明

In the first case, Johnny only has one ticket to distribute. The prizes are worth $ 4 $ and $ 5 $ , and the raffles initially have $ 1 $ and $ 2 $ tickets, respectively. After the first update, each raffle has $ 2 $ tickets, so Johnny has expected value  of winning by placing his ticket into the second raffle. The second update adds a ticket to the second raffle, so Johnny can win  in the first raffle. After the final update, Johnny keeps his ticket in the first raffle and wins . In the second case, Johnny has more tickets than he is allowed to spend. In particular, after the first update, there are $ 7 $ , $ 6 $ , and $ 6 $ tickets in each raffle, respectively, so Johnny can only put in $ 19 $ tickets, winning each prize with probability . Also, note that after the last two updates, Johnny must remove a ticket from the last raffle in order to stay under  the tickets in the third raffle.