Fix a Tree

题意翻译

对于下图中的树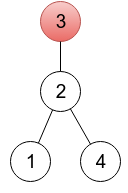，  可以用**数组**表示为 $[2,3,3,2]$。这种可以表示树的数组（即**有效**）需要符合以下条件： 1. 有且只有一个索引 $r$ ，符合 $p_r=r$ 。其中顶点 $r$ 是树的根。 2. 对于所有剩下的 $n-1$ 个顶点 $i$ 一定要有在 $i$ 和 $p_i$ 之间的边。 比如 数列 $(1,2,2)$、$(2,3,1)$ 和 $(2,1,3)$ 都是因为**根**的数目而导致不**有效**。 现在给你一个**数组** $a_1,a_2,\cdots ,a_n$，**不一定**是**有效**的。你需要对数组里面的值，通过**最小次数**的**更改**，使得这个数组**有效**。 并输出**最小更改次数**和一个通过最小更改次数而更改成功的**有效数组**。 如果有多种解，只需说出任何一组。 ### 输入格式 第一行是一个整数 $n\ (2\le n \le 200000)$ ----树的顶点个数。 第二行包含 $n$ 个整数 $a_1,a_2,\cdots ,a_n\ (1\le a_i\le n$。 ### 输出格式 第一行一个整数，**最小更改次数**。 第二行输出任意一个通过**最小更改次数**而更改成功的有效数组。 ## 说明 - 第一个样例只需要改一个就好啦！第一个样例输出是一个扎根于顶点 $4$ 的树（因为 $p_4=4$），你可以在下面的图中看到。另一个正确的答案应该是数列 $2,3,3,2$，扎根在顶点 $3$，也可以在下面的图中看到。两个图中顶点将用红色标出。 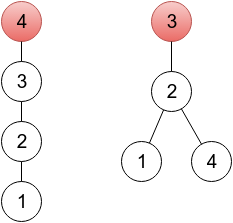 - 第二个样例中，给出的数列已经是有效的了。

题目描述

A tree is an undirected connected graph without cycles. Let's consider a rooted undirected tree with $ n $ vertices, numbered $ 1 $ through $ n $ . There are many ways to represent such a tree. One way is to create an array with $ n $ integers $ p_{1},p_{2},...,p_{n} $ , where $ p_{i} $ denotes a parent of vertex $ i $ (here, for convenience a root is considered its own parent). 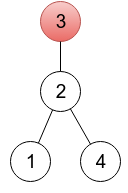 For this rooted tree the array $ p $ is $ [2,3,3,2] $ .Given a sequence $ p_{1},p_{2},...,p_{n} $ , one is able to restore a tree: 1. There must be exactly one index $ r $ that $ p_{r}=r $ . A vertex $ r $ is a root of the tree. 2. For all other $ n-1 $ vertices $ i $ , there is an edge between vertex $ i $ and vertex $ p_{i} $ . A sequence $ p_{1},p_{2},...,p_{n} $ is called valid if the described procedure generates some (any) rooted tree. For example, for $ n=3 $ sequences (1,2,2), (2,3,1) and (2,1,3) are not valid. You are given a sequence $ a_{1},a_{2},...,a_{n} $ , not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.

输入输出格式

输入格式

The first line of the input contains an integer $ n $ ( $ 2<=n<=200000 $ ) — the number of vertices in the tree. The second line contains $ n $ integers $ a_{1},a_{2},...,a_{n} $ ( $ 1<=a_{i}<=n $ ).

输出格式

In the first line print the minimum number of elements to change, in order to get a valid sequence. In the second line, print any valid sequence possible to get from $ (a_{1},a_{2},...,a_{n}) $ in the minimum number of changes. If there are many such sequences, any of them will be accepted.

输入输出样例

输入样例 #1

4
2 3 3 4

输出样例 #1

1
2 3 4 4 

输入样例 #2

5
3 2 2 5 3

输出样例 #2

0
3 2 2 5 3 

输入样例 #3

8
2 3 5 4 1 6 6 7

输出样例 #3

2
2 3 7 8 1 6 6 7

说明

In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex $ 4 $ (because $ p_{4}=4 $ ), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex $ 3 $ (right drawing below). On both drawings, roots are painted red. In the second sample, the given sequence is already valid.

题意翻译

对于下图中的树，  可以用**数组**表示为 $[2,3,3,2]$。这种可以表示树的数组（即**有效**）需要符合以下条件： 1. 有且只有一个索引 $r$ ，符合 $p_r=r$ 。其中顶点 $r$ 是树的根。 2. 对于所有剩下的 $n-1$ 个顶点 $i$ 一定要有在 $i$ 和 $p_i$ 之间的边。 比如 数列 $(1,2,2)$、$(2,3,1)$ 和 $(2,1,3)$ 都是因为**根**的数目而导致不**有效**。 现在给你一个**数组** $a_1,a_2,\cdots ,a_n$，**不一定**是**有效**的。你需要对数组里面的值，通过**最小次数**的**更改**，使得这个数组**有效**。 并输出**最小更改次数**和一个通过最小更改次数而更改成功的**有效数组**。 如果有多种解，只需说出任何一组。 ### 输入格式 第一行是一个整数 $n\ (2\le n \le 200000)$ ----树的顶点个数。 第二行包含 $n$ 个整数 $a_1,a_2,\cdots ,a_n\ (1\le a_i\le n$。 ### 输出格式 第一行一个整数，**最小更改次数**。 第二行输出任意一个通过**最小更改次数**而更改成功的有效数组。 ## 说明 - 第一个样例只需要改一个就好啦！第一个样例输出是一个扎根于顶点 $4$ 的树（因为 $p_4=4$），你可以在下面的图中看到。另一个正确的答案应该是数列 $2,3,3,2$，扎根在顶点 $3$，也可以在下面的图中看到。两个图中顶点将用红色标出。  - 第二个样例中，给出的数列已经是有效的了。