Sockets

题意翻译

## 题目描述 ICM ACPC 世界决赛就要来临了！不幸的是，赛事组织者因为在准备赛题时太忙碌了，他们几乎忘了一个关键点——为参赛者的工作站准备电力资源。 赛场有 $n$ 台为参赛者准备的电脑，第 $i$ 台电脑拥有与正整数 $p_i$ 相等大小的电源。同时，有 $m$ 个可用的插座，第 $j$ 个插座拥有与正整数 $s_j$ 相等的电源。只有当 $p_i = s_j$ 时才可以将第 $i$ 台电脑和第 $j$ 个插座连接。一台电脑只可以接一个插座。不仅如此，如果所有的电脑与插座的电源都不同，那么没有任何电脑可以接通至插座。 为了解决问题，Puch Williams 教授紧急订购了一车适配器（电源分离器）。每个适配器都有一个插头与一个插座，在它们之间还有一个分压器。在将适配器插入一个带有 $x$ 的电源后，适配器上的插座将会拥有一个 $\left \lceil \frac{x}{2} \right \rceil $ 的电源，这代表着将被插入的插座的电源除以 $2$，再取顶。例如：$\left \lceil \frac{10}{2} \right \rceil =5$，$\left \lceil \frac{15}{2} \right \rceil =8$。 每个适配器只能使用一次。它可以被多次串联。例如，在将一个适配器插入一个插入带有 $10$ 电源的插座的适配器时，可以将一个带有 $3$ 电源的电脑插入这个适配器。 组织者们会安装这些适配器，以确保它会同时输送给最多 $c$ 台电脑。如果有多种连接方案，组织者们想要在连接最多 $c$ 台电脑的前提下，使用最少 $u$ 个适配器的方案。 你的任务是帮助组织者们计算完成这个任务最大的 $c$ 和最小的 $u$。 这一车适配器是足够这个任务使用的，同时数据保证至少可以连接一台电脑。 ## 输入格式 第一行包含两个整数 $n$ 和 $m$（$1 \le n,m \le 200000$），分别为电脑的数量和插座的数量。 第二行包含 $n$ 个整数，$p_1,p_2,\ldots,p_n$（$1 \le p_i \le 10^9$），为电脑的电源。 第三行包含 $m$ 个整数，$s_1,s_2,\ldots,s_m$（$1 \le s_i \le 10^9$），为插座的电源。 ## 输出格式 第一行输出两个数字 $c$ 和 $u$，分别为最多可以连接的电脑数量与最少可以使用的适配器数量。 第二行输出 $m$ 个数字，$a_1,a_2,\ldots,a_m$（$0 \le a_i \le 10^9$），为插在第 $i$ 个插座上的适配器数量。$a_i$ 的和应等于 $u$。 第三行输出 $n$ 个数字，$b_1,b_2,\ldots,b_m$（$0 \le b_i \le m$），为第 $j$ 台电脑插入的插座序号。若 $b_j=0$，代表第 $j$ 台电脑不应插入任何插座。当 $b_j\ne 0$ 时，任何 $b_j$ 应不相等。在插入了 $a_{bj}$ 个适配器后，第 $j$ 台电脑的电源应与第 $b_j$ 个插座的电源相等。非 $0$ 的 $b_j$ 的数量应等于 $c$。 如果有多组答案，请输出任意一组。

题目描述

The ICM ACPC World Finals is coming! Unfortunately, the organizers of the competition were so busy preparing tasks that totally missed an important technical point — the organization of electricity supplement for all the participants workstations. There are $ n $ computers for participants, the $ i $ -th of which has power equal to positive integer $ p_{i} $ . At the same time there are $ m $ sockets available, the $ j $ -th of which has power euqal to positive integer $ s_{j} $ . It is possible to connect the $ i $ -th computer to the $ j $ -th socket if and only if their powers are the same: $ p_{i}=s_{j} $ . It is allowed to connect no more than one computer to one socket. Thus, if the powers of all computers and sockets are distinct, then no computer can be connected to any of the sockets. In order to fix the situation professor Puch Williams urgently ordered a wagon of adapters — power splitters. Each adapter has one plug and one socket with a voltage divider between them. After plugging an adapter to a socket with power $ x $ , the power on the adapter's socket becomes equal to 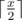, it means that it is equal to the socket's power divided by two with rounding up, for example 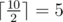 and 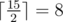. Each adapter can be used only once. It is possible to connect several adapters in a chain plugging the first to a socket. For example, if two adapters are plugged one after enother to a socket with power $ 10 $ , it becomes possible to connect one computer with power $ 3 $ to this socket. The organizers should install adapters so that it will be possible to supply with electricity the maximum number of computers $ c $ at the same time. If there are several possible connection configurations, they want to find the one that uses the minimum number of adapters $ u $ to connect $ c $ computers. Help organizers calculate the maximum number of connected computers $ c $ and the minimum number of adapters $ u $ needed for this. The wagon of adapters contains enough of them to do the task. It is guaranteed that it's possible to connect at least one computer.

输入输出格式

输入格式

The first line contains two integers $ n $ and $ m $ ( $ 1<=n,m<=200000 $ ) — the number of computers and the number of sockets. The second line contains $ n $ integers $ p_{1},p_{2},...,p_{n} $ ( $ 1<=p_{i}<=10^{9} $ ) — the powers of the computers. The third line contains $ m $ integers $ s_{1},s_{2},...,s_{m} $ ( $ 1<=s_{i}<=10^{9} $ ) — the power of the sockets.

输出格式

In the first line print two numbers $ c $ and $ u $ — the maximum number of computers which can at the same time be connected to electricity and the minimum number of adapters needed to connect $ c $ computers. In the second line print $ m $ integers $ a_{1},a_{2},...,a_{m} $ ( $ 0<=a_{i}<=10^{9} $ ), where $ a_{i} $ equals the number of adapters orginizers need to plug into the $ i $ -th socket. The sum of all $ a_{i} $ should be equal to $ u $ . In third line print $ n $ integers $ b_{1},b_{2},...,b_{n} $ ( $ 0<=b_{i}<=m $ ), where the $ b_{j} $ -th equals the number of the socket which the $ j $ -th computer should be connected to. $ b_{j}=0 $ means that the $ j $ -th computer should not be connected to any socket. All $ b_{j} $ that are different from $ 0 $ should be distinct. The power of the $ j $ -th computer should be equal to the power of the socket $ b_{j} $ after plugging in $ a_{bj} $ adapters. The number of non-zero $ b_{j} $ should be equal to $ c $ . If there are multiple answers, print any of them.

输入输出样例

输入样例 #1

2 2
1 1
2 2

输出样例 #1

2 2
1 1
1 2

输入样例 #2

2 1
2 100
99

输出样例 #2

1 6
6
1 0