Artsem and Saunders

题意翻译

### 题目描述 令 $ [n] $ 表示整数集 $ \{1,...,n\} $ ，令 $f:[x]\rightarrow[y]$ 表示函数 $f$ 的定义域为整数 $\{1,...,x\}$ 并且它的所有函数值在 $\{1,...,y\}$ 中。 现在，给定一个函数 $f:[x]\to[y]$ ，你的任务是找出一个正整数 $m$ ，和两个函数 $g:[n]\to[m]$、$h:[m]\to[n]$ ，满足对于任意 $x\in[m]$ ，有 $g(h(x))=x$ ；对于任意 $x\in[n]$ ，有 $h(g(x))=f(x)$ 。或者判定无解。 ### 输入格式 第一行一个正整数 $n$ ，第二行 $n$ 个正整数，第 $i$ 个数表示 $f(i)$ 的值。 ### 输出格式 如果无解，输出 $-1$ 。 否则，第一行输出 $m$ ，第二行输出 $n$ 个整数，第 $i$ 个数为 $g(i)$ ，第三行输出 $m$ 个整数，第 $i$ 个数为 $h(i)$ 。 如果有多组可行解，只需输出一组即可。

题目描述

Artsem has a friend Saunders from University of Chicago. Saunders presented him with the following problem. Let $ [n] $ denote the set $ {1,...,n} $ . We will also write $ f:[x]→[y] $ when a function $ f $ is defined in integer points $ 1 $ , ..., $ x $ , and all its values are integers from 1 to $ y $ . Now then, you are given a function $ f:[n]→[n] $ . Your task is to find a positive integer $ m $ , and two functions $ g:[n]→[m] $ , $ h:[m]→[n] $ , such that $ g(h(x))=x $ for all 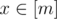, and $ h(g(x))=f(x) $ for all , or determine that finding these is impossible.

输入输出格式

输入格式

The first line contains an integer $ n $ ( $ 1<=n<=10^{5} $ ). The second line contains $ n $ space-separated integers — values $ f(1),...,f(n) $ ( $ 1<=f(i)<=n $ ).

输出格式

If there is no answer, print one integer -1. Otherwise, on the first line print the number $ m $ ( $ 1<=m<=10^{6} $ ). On the second line print $ n $ numbers $ g(1),...,g(n) $ . On the third line print $ m $ numbers $ h(1),...,h(m) $ . If there are several correct answers, you may output any of them. It is guaranteed that if a valid answer exists, then there is an answer satisfying the above restrictions.

输入输出样例

输入样例 #1

3
1 2 3

输出样例 #1

3
1 2 3
1 2 3

输入样例 #2

3
2 2 2

输出样例 #2

1
1 1 1
2

输入样例 #3

2
2 1

输出样例 #3

-1

题意翻译

### 题目描述 令 $ [n] $ 表示整数集 $ \{1,...,n\} $ ，令 $f:[x]\rightarrow[y]$ 表示函数 $f$ 的定义域为整数 $\{1,...,x\}$ 并且它的所有函数值在 $\{1,...,y\}$ 中。 现在，给定一个函数 $f:[x]\to[y]$ ，你的任务是找出一个正整数 $m$ ，和两个函数 $g:[n]\to[m]$、$h:[m]\to[n]$ ，满足对于任意 $x\in[m]$ ，有 $g(h(x))=x$ ；对于任意 $x\in[n]$ ，有 $h(g(x))=f(x)$ 。或者判定无解。 ### 输入格式 第一行一个正整数 $n$ ，第二行 $n$ 个正整数，第 $i$ 个数表示 $f(i)$ 的值。 ### 输出格式 如果无解，输出 $-1$ 。 否则，第一行输出 $m$ ，第二行输出 $n$ 个整数，第 $i$ 个数为 $g(i)$ ，第三行输出 $m$ 个整数，第 $i$ 个数为 $h(i)$ 。 如果有多组可行解，只需输出一组即可。