Surprise me!

题意翻译

给定一棵 $n$ 个节点的树，每个点有一个权值 $a[i]$ ，保证 $a[i]$ 是一个 $1..n$ 的排列。 求 $\frac{1}{n(n-1)}\sum_{i=1}^n\sum_{j\ne i}\varphi(a_i*a_j)* dist(i,j)$ 其中， $\varphi(x)$ 是欧拉函数， $dist(i,j)$ 表示 $i,j$ 两个节点在树上的距离。 感谢@yybyyb 提供的翻译

题目描述

Tired of boring dates, Leha and Noora decided to play a game. Leha found a tree with $ n $ vertices numbered from $ 1 $ to $ n $ . We remind you that tree is an undirected graph without cycles. Each vertex $ v $ of a tree has a number $ a_{v} $ written on it. Quite by accident it turned out that all values written on vertices are distinct and are natural numbers between $ 1 $ and $ n $ . The game goes in the following way. Noora chooses some vertex $ u $ of a tree uniformly at random and passes a move to Leha. Leha, in his turn, chooses (also uniformly at random) some vertex $ v $ from remaining vertices of a tree $ (v≠u) $ . As you could guess there are $ n(n-1) $ variants of choosing vertices by players. After that players calculate the value of a function $ f(u,v)=φ(a_{u}·a_{v}) $ $ · $ $ d(u,v) $ of the chosen vertices where $ φ(x) $ is Euler's totient function and $ d(x,y) $ is the shortest distance between vertices $ x $ and $ y $ in a tree. Soon the game became boring for Noora, so Leha decided to defuse the situation and calculate expected value of function $ f $ over all variants of choosing vertices $ u $ and $ v $ , hoping of at least somehow surprise the girl. Leha asks for your help in calculating this expected value. Let this value be representable in the form of an irreducible fraction 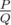. To further surprise Noora, he wants to name her the value 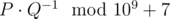. Help Leha!

输入输出格式

输入格式

The first line of input contains one integer number $ n $ $ (2<=n<=2·10^{5}) $ — number of vertices in a tree. The second line contains $ n $ different numbers $ a_{1},a_{2},...,a_{n} $ $ (1<=a_{i}<=n) $ separated by spaces, denoting the values written on a tree vertices. Each of the next $ n-1 $ lines contains two integer numbers $ x $ and $ y $ $ (1<=x,y<=n) $ , describing the next edge of a tree. It is guaranteed that this set of edges describes a tree.

输出格式

In a single line print a number equal to $ P·Q^{-1} $ modulo $ 10^{9}+7 $ .

输入输出样例

输入样例 #1

3
1 2 3
1 2
2 3

输出样例 #1

333333338

输入样例 #2

5
5 4 3 1 2
3 5
1 2
4 3
2 5

输出样例 #2

8

说明

Euler's totient function $ φ(n) $ is the number of such $ i $ that $ 1<=i<=n $ ,and $ gcd(i,n)=1 $ , where $ gcd(x,y) $ is the greatest common divisor of numbers $ x $ and $ y $ . There are $ 6 $ variants of choosing vertices by Leha and Noora in the first testcase: - $ u=1 $ , $ v=2 $ , $ f(1,2)=φ(a_{1}·a_{2})·d(1,2)=φ(1·2)·1=φ(2)=1 $ - $ u=2 $ , $ v=1 $ , $ f(2,1)=f(1,2)=1 $ - $ u=1 $ , $ v=3 $ , $ f(1,3)=φ(a_{1}·a_{3})·d(1,3)=φ(1·3)·2=2φ(3)=4 $ - $ u=3 $ , $ v=1 $ , $ f(3,1)=f(1,3)=4 $ - $ u=2 $ , $ v=3 $ , $ f(2,3)=φ(a_{2}·a_{3})·d(2,3)=φ(2·3)·1=φ(6)=2 $ - $ u=3 $ , $ v=2 $ , $ f(3,2)=f(2,3)=2 $ Expected value equals to . The value Leha wants to name Noora is $ 7·3^{-1}=7·333333336=333333338 $ . In the second testcase expected value equals to , so Leha will have to surprise Hoora by number $ 8·1^{-1}=8 $ .