Madness

题意翻译

给出一个 $n$ 个节点的树。 你需要选出若干条简单路径，且路径两两无公共**边**，每个点至少被一条路径覆盖。 每条路径上都会有一个人沿着路径以每秒一条边的速度无限来回移动（若到达路径端点则改变方向），你可以任意决定他的初始位置和初始方向。初始位置可以在边上的任意一个位置。 每个点上都有一个计时器，永远不会停止计数。当某个人经过这个点，这个点上的计时器计数会重置至 $0$。 记 $res_v$ 表示点 $v$ 上计时器表示的最大计数，则你需要通过合理选择路径、安排行走的人员，使得序列 $\{res_1, res_2, \ldots, res_n\}$ 的**字典序**最小。

题目描述

The second semester starts at the University of Pavlopolis. After vacation in Vičkopolis Noora needs to return to Pavlopolis and continue her study. Sometimes (or quite often) there are teachers who do not like you. Incidentally Noora also has one such teacher. His name is Yury Dmitrievich and he teaches graph theory. Yury Dmitrievich doesn't like Noora, so he always gives the girl the most difficult tasks. So it happened this time. The teacher gives Noora a tree with $ n $ vertices. Vertices are numbered with integers from $ 1 $ to $ n $ . The length of all the edges of this tree is $ 1 $ . Noora chooses a set of simple paths that pairwise don't intersect in edges. However each vertex should belong to at least one of the selected path. For each of the selected paths, the following is done: 1. We choose exactly one edge $ (u,v) $ that belongs to the path. 2. On the selected edge $ (u,v) $ there is a point at some selected distance $ x $ from the vertex $ u $ and at distance $ 1-x $ from vertex $ v $ . But the distance $ x $ chosen by Noora arbitrarily, i. e. it can be different for different edges. 3. One of the vertices $ u $ or $ v $ is selected. The point will start moving to the selected vertex. Let us explain how the point moves by example. Suppose that the path consists of two edges $ (v_{1},v_{2}) $ and $ (v_{2},v_{3}) $ , the point initially stands on the edge $ (v_{1},v_{2}) $ and begins its movement to the vertex $ v_{1} $ . Then the point will reach $ v_{1} $ , then "turn around", because the end of the path was reached, further it will move in another direction to vertex $ v_{2} $ , then to vertex $ v_{3} $ , then "turn around" again, then move to $ v_{2} $ and so on. The speed of the points is $ 1 $ edge per second. For example, for $ 0.5 $ second the point moves to the length of the half of an edge. A stopwatch is placed at each vertex of the tree. The time that the stopwatches indicate at start time is $ 0 $ seconds. Then at the starting moment of time, all points simultaneously start moving from the selected positions to selected directions along the selected paths, and stopwatches are simultaneously started. When one of the points reaches the vertex $ v $ , the stopwatch at the vertex $ v $ is automatically reset, i.e. it starts counting the time from zero. Denote by $ res_{v} $ the maximal time that the stopwatch at the vertex $ v $ will show if the point movement continues infinitely. Noora is asked to select paths and points on them so that $ res_{1} $ is as minimal as possible. If there are several solutions to do this, it is necessary to minimize $ res_{2} $ , then $ res_{3} $ , $ res_{4},...,res_{n} $ . Help Noora complete the teacher's task. For the better understanding of the statement, see the explanation for the example.

输入输出格式

输入格式

The first line contains single integer $ n $ ( $ 2<=n<=100 $ ) — number of vertices in the given tree. Each of next $ n-1 $ lines contains two integers $ u $ and $ v $ ( $ 1<=u,v<=n,u≠v $ ) — vertices connected by an edge. Guaranteed that input defines a valid tree.

输出格式

In the first line print single integer $ paths $ — number of paths you want to choose. In the next $ paths $ lines print path's descriptions: 1. Single integer $ len $ — number of edges in the current path. 2. $ len $ integers — indices of the edges in the path. The edges are numbered from $ 1 $ to $ n-1 $ in order they are given in input. 3. Two integers $ u $ and $ v $ — means that you put point on the edge between vertices $ u $ and $ v $ (obviously the edge should belong to the path) and a point will start moving to the vertex $ v $ . Note that order of printing of the edge's ends is important. For example if you print "1 2" (without quotes), then point will start moving to vertex $ 2 $ ; but if you print "2 1" (without quotes), then point will start moving to vertex $ 1 $ . 4. Single real number $ x $ ( $ 0<=x<=1 $ ) — distance between point and vertex $ u $ (the same vertex that you print first in the third paragraph). Scoring Judge system will generate array $ res $ using the output data provided by the participant. Also system will generate array $ resOptimal $ by the jury answer. Your answer will be accepted if only for each $ i $ ( $ 1<=i<=n $ ) the following is satisfied: .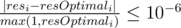

输入输出样例

输入样例 #1

3
1 2
2 3

输出样例 #1

2
1 1 1 2 0.6666666666
1 2 2 3 0.6666666666

说明

Consider an example. In starting moment of time points are located as following:  The first path is highlighted in red, the second in blue, green circles represent chosen points, and brown numbers inside vertices — current time at stopwatch. Purple arrows represent direction in which points will move. In $ 0.(3) $ seconds points will be located in following way (before stopwatch reset):  After stopwatch reset:  In $ 1.0 $ second after the start of moving:  In $ 1.(3) $ seconds after the start of moving (after stopwatch reset):  Finally, in $ 2 $ seconds after the start of moving points return to their initial positions.  This process will continue infinitely.

题意翻译

给出一个 $n$ 个节点的树。 你需要选出若干条简单路径，且路径两两无公共**边**，每个点至少被一条路径覆盖。 每条路径上都会有一个人沿着路径以每秒一条边的速度无限来回移动（若到达路径端点则改变方向），你可以任意决定他的初始位置和初始方向。初始位置可以在边上的任意一个位置。 每个点上都有一个计时器，永远不会停止计数。当某个人经过这个点，这个点上的计时器计数会重置至 $0$。 记 $res_v$ 表示点 $v$ 上计时器表示的最大计数，则你需要通过合理选择路径、安排行走的人员，使得序列 $\{res_1, res_2, \ldots, res_n\}$ 的**字典序**最小。