Property

题意翻译

有一个正 $2n$ 边形，在每条边上有 $n$ 等分点。现在已经选定了 $n$ 个点，第 $i$个点分别位于第 $2i+1$ 条边上，且这 $n$ 个点的序号构成了一个排列；你需要再选出 $n$ 个点位于第 $2i$ 条边上，并且这 $n$ 个点的序号也构成一个排列，使得这些点构成的多边形面积最大。

题目描述

Bill is a famous mathematician in BubbleLand. Thanks to his revolutionary math discoveries he was able to make enough money to build a beautiful house. Unfortunately, for not paying property tax on time, court decided to punish Bill by making him lose a part of his property. Bill’s property can be observed as a convex regular $ 2n $ -sided polygon $ A_{0}\ A_{1}...\ A_{2n-1}\ A_{2n},\ A_{2n}=\ A_{0} $ , with sides of the exactly 1 meter in length. Court rules for removing part of his property are as follows: - Split every edge $ A_{k}\ A_{k+1},\ k=0...\ 2n-1 $ in $ n $ equal parts of size $ 1/n $ with points $ P_{0},P_{1},...,P_{n-1} $ - On every edge $ A_{2k}\ A_{2k+1},\ k=0...\ n-1 $ court will choose one point $ B_{2k}=\ P_{i} $ for some $ i=0,...,\ n-1 $ such that 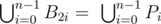 - On every edge $ A_{2k+1}A_{2k+2},\ k=0...n-1 $ Bill will choose one point $ B_{2k+1}=\ P_{i} $ for some $ i=0,...,\ n-1 $ such that 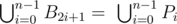 - Bill gets to keep property inside of $ 2n $ -sided polygon $ B_{0}\ B_{1}...\ B_{2n-1} $ Luckily, Bill found out which $ B_{2k} $ points the court chose. Even though he is a great mathematician, his house is very big and he has a hard time calculating. Therefore, he is asking you to help him choose points so he maximizes area of property he can keep.

输入输出格式

输入格式

The first line contains one integer number $ n\ (2<=n<=50000) $ , representing number of edges of $ 2n $ -sided polygon. The second line contains $ n $ distinct integer numbers $ B_{2k}\ (0<=B_{2k}<=n-1,\ k=0...\ n-1) $ separated by a single space, representing points the court chose. If $ B_{2k}=i $ , the court chose point $ P_{i} $ on side $ A_{2k}\ A_{2k+1} $ .

输出格式

Output contains $ n $ distinct integers separated by a single space representing points $ B_{1},B_{3},...,B_{2n-1} $ Bill should choose in order to maximize the property area. If there are multiple solutions that maximize the area, return any of them.

输入输出样例

输入样例 #1

3
0 1 2

输出样例 #1

0 2 1

说明

To maximize area Bill should choose points: $ B_{1}=P_{0} $ , $ B_{3}=P_{2} $ , $ B_{5}=P_{1} $ 

题意翻译

有一个正 $2n$ 边形，在每条边上有 $n$ 等分点。现在已经选定了 $n$ 个点，第 $i$个点分别位于第 $2i+1$ 条边上，且这 $n$ 个点的序号构成了一个排列；你需要再选出 $n$ 个点位于第 $2i$ 条边上，并且这 $n$ 个点的序号也构成一个排列，使得这些点构成的多边形面积最大。