Third Month Insanity

题意翻译

有$ 2^n $个人要进行比赛，每次$ 2i $与$ 2i+1 $号人进行比赛$(i\in [0,2^{n-1}))$。这一轮中赢的人进入下一轮。下一轮比赛的时候把进入这一轮的人按编号排好，仍然是像之前那样相邻的进行一次比赛。最后只剩下一个人。 数据给出对于$ x,y$，$x $打赢$ y $的概率。 第$ i $轮比赛会角逐出$ 2^{n-i} $个赢家。我们要在比赛开始前，猜每轮的赢家（一轮的赢家一定要是上一轮的赢家）。第$ i $轮每猜中一个赢家就会得到$ 2^{i-1} $的得分。 求最大的期望得分。$n \leqslant 6$

题目描述

The annual college sports-ball tournament is approaching, which for trademark reasons we'll refer to as Third Month Insanity. There are a total of $ 2^{N} $ teams participating in the tournament, numbered from $ 1 $ to $ 2^{N} $ . The tournament lasts $ N $ rounds, with each round eliminating half the teams. The first round consists of $ 2^{N-1} $ games, numbered starting from $ 1 $ . In game $ i $ , team $ 2·i-1 $ will play against team $ 2·i $ . The loser is eliminated and the winner advances to the next round (there are no ties). Each subsequent round has half as many games as the previous round, and in game $ i $ the winner of the previous round's game $ 2·i-1 $ will play against the winner of the previous round's game $ 2·i $ . Every year the office has a pool to see who can create the best bracket. A bracket is a set of winner predictions for every game. For games in the first round you may predict either team to win, but for games in later rounds the winner you predict must also be predicted as a winner in the previous round. Note that the bracket is fully constructed before any games are actually played. Correct predictions in the first round are worth $ 1 $ point, and correct predictions in each subsequent round are worth twice as many points as the previous, so correct predictions in the final game are worth $ 2^{N-1} $ points. For every pair of teams in the league, you have estimated the probability of each team winning if they play against each other. Now you want to construct a bracket with the maximum possible expected score.

输入输出格式

输入格式

Input will begin with a line containing $ N $ ( $ 2<=N<=6 $ ). $ 2^{N} $ lines follow, each with $ 2^{N} $ integers. The $ j $ -th column of the $ i $ -th row indicates the percentage chance that team $ i $ will defeat team $ j $ , unless $ i=j $ , in which case the value will be $ 0 $ . It is guaranteed that the $ i $ -th column of the $ j $ -th row plus the $ j $ -th column of the $ i $ -th row will add to exactly $ 100 $ .

输出格式

Print the maximum possible expected score over all possible brackets. Your answer must be correct to within an absolute or relative error of $ 10^{-9} $ . Formally, let your answer be $ a $ , and the jury's answer be $ b $ . Your answer will be considered correct, if .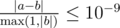

输入输出样例

输入样例 #1

2
0 40 100 100
60 0 40 40
0 60 0 45
0 60 55 0

输出样例 #1

1.75

输入样例 #2

3
0 0 100 0 100 0 0 0
100 0 100 0 0 0 100 100
0 0 0 100 100 0 0 0
100 100 0 0 0 0 100 100
0 100 0 100 0 0 100 0
100 100 100 100 100 0 0 0
100 0 100 0 0 100 0 0
100 0 100 0 100 100 100 0

输出样例 #2

12

输入样例 #3

2
0 21 41 26
79 0 97 33
59 3 0 91
74 67 9 0

输出样例 #3

3.141592

说明

In the first example, you should predict teams $ 1 $ and $ 4 $ to win in round $ 1 $ , and team $ 1 $ to win in round $ 2 $ . Recall that the winner you predict in round $ 2 $ must also be predicted as a winner in round $ 1 $ .

题意翻译

有$ 2^n $个人要进行比赛，每次$ 2i $与$ 2i+1 $号人进行比赛$(i\in [0,2^{n-1}))$。这一轮中赢的人进入下一轮。下一轮比赛的时候把进入这一轮的人按编号排好，仍然是像之前那样相邻的进行一次比赛。最后只剩下一个人。 数据给出对于$ x,y$，$x $打赢$ y $的概率。 第$ i $轮比赛会角逐出$ 2^{n-i} $个赢家。我们要在比赛开始前，猜每轮的赢家（一轮的赢家一定要是上一轮的赢家）。第$ i $轮每猜中一个赢家就会得到$ 2^{i-1} $的得分。 求最大的期望得分。$n \leqslant 6$