New Year and Arbitrary Arrangement

题意翻译

给定三个数 $k,pa,pb$。 每次有 $\dfrac{pa}{pa+pb}$ 的概率往后面添加一个 `a`。 每次有 $\dfrac{pb}{pa+pb}$ 的概率往后面添加一个 `b`。 当出现了 $k$ 个形如 $ab$ 的子序列（不用连续）时停止。 求最后 `ab` 序列的期望数。 答案对 $10^9+7$ 取模。 Translated by yybyyb

题目描述

You are given three integers $ k $ , $ p_{a} $ and $ p_{b} $ . You will construct a sequence with the following algorithm: Initially, start with the empty sequence. Each second, you do the following. With probability $ p_{a}/(p_{a}+p_{b}) $ , add 'a' to the end of the sequence. Otherwise (with probability $ p_{b}/(p_{a}+p_{b}) $ ), add 'b' to the end of the sequence. You stop once there are at least $ k $ subsequences that form 'ab'. Determine the expected number of times 'ab' is a subsequence in the resulting sequence. It can be shown that this can be represented by $ P/Q $ , where $ P $ and $ Q $ are coprime integers, and 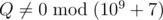. Print the value of .

输入输出格式

输入格式

The first line will contain three integers integer $ k,p_{a},p_{b} $ ( $ 1<=k<=1000 $ , $ 1<=p_{a},p_{b}<=1000000 $ ).

输出格式

Print a single integer, the answer to the problem.

输入输出样例

输入样例 #1

1 1 1

输出样例 #1

2

输入样例 #2

3 1 4

输出样例 #2

370000006

说明

The first sample, we will keep appending to our sequence until we get the subsequence 'ab' at least once. For instance, we get the sequence 'ab' with probability 1/4, 'bbab' with probability 1/16, and 'aab' with probability 1/8. Note, it's impossible for us to end with a sequence like 'aabab', since we would have stopped our algorithm once we had the prefix 'aab'. The expected amount of times that 'ab' will occur across all valid sequences is 2. For the second sample, the answer is equal to .

题意翻译

给定三个数 $k,pa,pb$。 每次有 $\dfrac{pa}{pa+pb}$ 的概率往后面添加一个 `a`。 每次有 $\dfrac{pb}{pa+pb}$ 的概率往后面添加一个 `b`。 当出现了 $k$ 个形如 $ab$ 的子序列（不用连续）时停止。 求最后 `ab` 序列的期望数。 答案对 $10^9+7$ 取模。 Translated by yybyyb