Modular Exponentiation

题意翻译

给定n,m，求$m\ mod\ 2^n$

题目描述

The following problem is well-known: given integers $ n $ and $ m $ , calculate 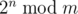, where $ 2^{n}=2·2·...·2 $ ( $ n $ factors), and 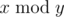 denotes the remainder of division of $ x $ by $ y $ . You are asked to solve the "reverse" problem. Given integers $ n $ and $ m $ , calculate .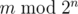

输入输出格式

输入格式

The first line contains a single integer $ n $ ( $ 1<=n<=10^{8} $ ). The second line contains a single integer $ m $ ( $ 1<=m<=10^{8} $ ).

输出格式

Output a single integer — the value of .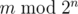

输入输出样例

输入样例 #1

4
42

输出样例 #1

10

输入样例 #2

1
58

输出样例 #2

0

输入样例 #3

98765432
23456789

输出样例 #3

23456789

说明

In the first example, the remainder of division of 42 by $ 2^{4}=16 $ is equal to 10. In the second example, 58 is divisible by $ 2^{1}=2 $ without remainder, and the answer is 0.