304808: CF915G. Coprime Arrays
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Coprime Arrays
题意翻译
#### 题意: 我们称一个大小为 $n$ 的数组 $a$ 互质,当且仅当 $gcd(a_1,a_2,\cdots,a_n)=1$,$gcd$ 是最大公约数的意思。 给定 $n,k$,对于每个 $i$ $(1\le i\le k)$,你都需要确定这样的数组的个数——长度为 $n$ 的互质数组 $a$ ,满足对每个 $j$ $(1\le j\le n)$,都有 $1\le a_j\le i$。 答案可能非常大,请对 $10^9+7$ 取模。 #### 输入格式: 只有一行,两个数 $n,k$ $(1\le n,k\le 2\cdot10^6)$,分别表示数组的大小和数组元素大小的上限。 #### 输出格式: 为了降低输出的时间,你需要对输出进行如下处理: 把 $i$ 的答案(对 $10^9+7$ 取模后)记作 $b_i$。你需要输出 $\sum_{i=1}^{k} (b_i\oplus i)$,再对 $10^9+7$ 取模。 这里 $\oplus$ 表示按位异或,在 c++ 和 Java 中写作 ```^```,在 Pascal 中写作 ```xor```。 #### 说明: 第一个样例的说明: 因为互质数组的数量比较多,我们只列出不互质的: 当 $i=1$ 时,唯一的数组就是互质的,$b_1=1$。 当 $i=2$ 时,数组 $[2,2,2]$ 不是互质的,$b_2=7$。 当 $i=3$ 时,数组 $[2,2,2],[3,3,3]$ 不是互质的,$b_3=25$。 当 $i=4$ 时,数组 $[2,2,2],[3,3,3],[2,2,4],[2,4,2],[2,4,4],[4,2,2],[4,2,4],[4,4,2],[4,4,4]$ 不是互质的,$b_4=55$。 Translated by 小粉兔题目描述
Let's call an array $ a $ of size $ n $ coprime iff $ gcd(a_{1},a_{2},...,a_{n})=1 $ , where $ gcd $ is the greatest common divisor of the arguments. You are given two numbers $ n $ and $ k $ . For each $ i $ ( $ 1<=i<=k $ ) you have to determine the number of coprime arrays $ a $ of size $ n $ such that for every $ j $ ( $ 1<=j<=n $ ) $ 1<=a_{j}<=i $ . Since the answers can be very large, you have to calculate them modulo $ 10^{9}+7 $ .输入输出格式
输入格式
The first line contains two integers $ n $ and $ k $ ( $ 1<=n,k<=2·10^{6} $ ) — the size of the desired arrays and the maximum upper bound on elements, respectively.
输出格式
Since printing $ 2·10^{6} $ numbers may take a lot of time, you have to output the answer in such a way: Let $ b_{i} $ be the number of coprime arrays with elements in range $ [1,i] $ , taken modulo $ 10^{9}+7 $ . You have to print 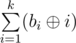, taken modulo $ 10^{9}+7 $ . Here  denotes bitwise xor operation (^ in C++ or Java, xor in Pascal).
输入输出样例
输入样例 #1
3 4
输出样例 #1
82
输入样例 #2
2000000 8
输出样例 #2
339310063