Jamie and Binary Sequence (changed after round)

题意翻译

把一个数分解成**恰好** $k$ 个 $2^{a_i}$ 次方的和，可以重复，要求保证最大的 $a_i$ 要尽可能的小时，$a$ 的字典序尽可能大，输出序列 $a$。

题目描述

Jamie is preparing a Codeforces round. He has got an idea for a problem, but does not know how to solve it. Help him write a solution to the following problem: Find $ k $ integers such that the sum of two to the power of each number equals to the number $ n $ and the largest integer in the answer is as small as possible. As there may be multiple answers, you are asked to output the lexicographically largest one. To be more clear, consider all integer sequence with length $ k $ $ (a_{1},a_{2},...,a_{k}) $ with 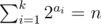. Give a value 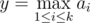 to each sequence. Among all sequence(s) that have the minimum $ y $ value, output the one that is the lexicographically largest. For definitions of powers and lexicographical order see notes.

输入输出格式

输入格式

The first line consists of two integers $ n $ and $ k $ ( $ 1<=n<=10^{18},1<=k<=10^{5}) $ — the required sum and the length of the sequence.

输出格式

Output "No" (without quotes) in a single line if there does not exist such sequence. Otherwise, output "Yes" (without quotes) in the first line, and $ k $ numbers separated by space in the second line — the required sequence. It is guaranteed that the integers in the answer sequence fit the range $ [-10^{18},10^{18}] $ .

输入输出样例

输入样例 #1

23 5

输出样例 #1

Yes
3 3 2 1 0 

输入样例 #2

13 2

输出样例 #2

No

输入样例 #3

1 2

输出样例 #3

Yes
-1 -1 

说明

Sample 1: $ 2^{3}+2^{3}+2^{2}+2^{1}+2^{0}=8+8+4+2+1=23 $ Answers like $ (3,3,2,0,1) $ or $ (0,1,2,3,3) $ are not lexicographically largest. Answers like $ (4,1,1,1,0) $ do not have the minimum $ y $ value. Sample 2: It can be shown there does not exist a sequence with length 2. Sample 3:  Powers of 2: If $ x>0 $ , then $ 2^{x}=2·2·2·...·2 $ ( $ x $ times). If $ x=0 $ , then $ 2^{x}=1 $ . If $ x<0 $ , then . Lexicographical order: Given two different sequences of the same length, $ (a_{1},a_{2},...\ ,a_{k}) $ and $ (b_{1},b_{2},...\ ,b_{k}) $ , the first one is smaller than the second one for the lexicographical order, if and only if $ a_{i}<b_{i} $ , for the first $ i $ where $ a_{i} $ and $ b_{i} $ differ.

题意翻译

把一个数分解成**恰好** $k$ 个 $2^{a_i}$ 次方的和，可以重复，要求保证最大的 $a_i$ 要尽可能的小时，$a$ 的字典序尽可能大，输出序列 $a$。