A Determined Cleanup

题意翻译

一个多项式函数 $f(x)$，系数为非负整数，然后可以拆成 $f(x)=q(x)\cdot(x+k)+p$ 的形式，且 $q(x)$ 也是一个多项式函数，但是系数没有要求。现在告诉你 $k$ 和 $p$，问是否存在这样一个 $f(x)$，且 $f(x)$ 的系数小于 $k$。

题目描述

In order to put away old things and welcome a fresh new year, a thorough cleaning of the house is a must. Little Tommy finds an old polynomial and cleaned it up by taking it modulo another. But now he regrets doing this... Given two integers $ p $ and $ k $ , find a polynomial $ f(x) $ with non-negative integer coefficients strictly less than $ k $ , whose remainder is $ p $ when divided by $ (x+k) $ . That is, $ f(x)=q(x)·(x+k)+p $ , where $ q(x) $ is a polynomial (not necessarily with integer coefficients).

输入输出格式

输入格式

The only line of input contains two space-separated integers $ p $ and $ k $ ( $ 1<=p<=10^{18} $ , $ 2<=k<=2000 $ ).

输出格式

If the polynomial does not exist, print a single integer -1, or output two lines otherwise. In the first line print a non-negative integer $ d $ — the number of coefficients in the polynomial. In the second line print $ d $ space-separated integers $ a_{0},a_{1},...,a_{d-1} $ , describing a polynomial 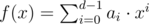 fulfilling the given requirements. Your output should satisfy $ 0<=a_{i}&lt;k $ for all $ 0<=i<=d-1 $ , and $ a_{d-1}≠0 $ . If there are many possible solutions, print any of them.

输入输出样例

输入样例 #1

46 2

输出样例 #1

7
0 1 0 0 1 1 1

输入样例 #2

2018 214

输出样例 #2

3
92 205 1

说明

In the first example, $ f(x)=x^{6}+x^{5}+x^{4}+x=(x^{5}-x^{4}+3x^{3}-6x^{2}+12x-23)·(x+2)+46 $ . In the second example, $ f(x)=x^{2}+205x+92=(x-9)·(x+214)+2018 $ .