Circles of Waiting

题意翻译

在平面直角坐标系上，有一个神奇的点，一开始在 $(0, 0)$ 。每秒钟这个点都会随机移动：如果它在 $(x, y)$ ，下一秒它在 $(x - 1, y)$ 的概率是 $p_1$ ，在 $(x, y - 1)$ 的概率是 $p_2$ ，在 $(x + 1, y)$ 的概率是 $p_3$ ，在 $(x, y + 1)$ 的概率是 $p_4$ 。保证 $p_1 + p_2 + p_3 + p_4 = 1$ ，各次移动互不关联。 求出这个点移动至距离原点距离为大于 $R$ 的点的期望步数。距离为欧几里得距离。 感谢@OrangeLee 提供的翻译

题目描述

A chip was placed on a field with coordinate system onto point $ (0,0) $ . Every second the chip moves randomly. If the chip is currently at a point $ (x,y) $ , after a second it moves to the point $ (x-1,y) $ with probability $ p_{1} $ , to the point $ (x,y-1) $ with probability $ p_{2} $ , to the point $ (x+1,y) $ with probability $ p_{3} $ and to the point $ (x,y+1) $ with probability $ p_{4} $ . It's guaranteed that $ p_{1}+p_{2}+p_{3}+p_{4}=1 $ . The moves are independent. Find out the expected time after which chip will move away from origin at a distance greater than $ R $ (i.e. 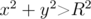 will be satisfied).

输入输出格式

输入格式

First line contains five integers $ R,a_{1},a_{2},a_{3} $ and $ a_{4} $ ( $ 0<=R<=50,1<=a_{1},a_{2},a_{3},a_{4}<=1000 $ ). Probabilities $ p_{i} $ can be calculated using formula .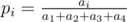

输出格式

It can be shown that answer for this problem is always a rational number of form 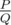, where 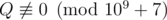. Print $ P·Q^{-1} $ modulo $ 10^{9}+7 $ .

输入输出样例

输入样例 #1

0 1 1 1 1

输出样例 #1

1

输入样例 #2

1 1 1 1 1

输出样例 #2

666666674

输入样例 #3

1 1 2 1 2

输出样例 #3

538461545

说明

In the first example initially the chip is located at a distance $ 0 $ from origin. In one second chip will move to distance $ 1 $ is some direction, so distance to origin will become $ 1 $ . Answers to the second and the third tests:  and .

题意翻译

在平面直角坐标系上，有一个神奇的点，一开始在 $(0, 0)$ 。每秒钟这个点都会随机移动：如果它在 $(x, y)$ ，下一秒它在 $(x - 1, y)$ 的概率是 $p_1$ ，在 $(x, y - 1)$ 的概率是 $p_2$ ，在 $(x + 1, y)$ 的概率是 $p_3$ ，在 $(x, y + 1)$ 的概率是 $p_4$ 。保证 $p_1 + p_2 + p_3 + p_4 = 1$ ，各次移动互不关联。 求出这个点移动至距离原点距离为大于 $R$ 的点的期望步数。距离为欧几里得距离。 感谢@OrangeLee 提供的翻译