Minimal k-covering

题意翻译

##### 题目大意 给你一张二分图 $G = (U, V, E)$ ， $U$ 是图的 $X$ 部， $V$ 是图的 $Y$ 部， $E$ 是边集，可能有重边。 我们称 $E$ 的某个子集 $\overline E$ 是 *k-覆盖* 的，当且仅当图 $\overline G = (U, V, \overline E)$ 的每个顶点至少连接了 $k$ 条边；若 $\overline E$ 是 k-覆盖 的且不存在元素个数比它更小的边集也是 k-覆盖 的，则称 $\overline E$ 是一个 *最小k-覆盖* 。 你的任务是对于所有 $k \in [0, minDegree]$ ，求出 最小k-覆盖，其中 $minDegree$ 是图 $G$ 的所有点度数的最小值。 ###### 输入格式 第一行输入三个整数 $n_1$ ， $n_2$ 和 $m$ （ $1 \le n_1, n_2 \le 2000$ ， $0 \le m \le 2000$ ），分别代表 $U$ 的点数， $V$ 的点数和边数。 接下来 $m$ 行每行两个整数 $u_i$ 和 $v_i$ ，表示第 $i$ 条边在 $U$ 中的端点为 $u_i$ ，在 $V$ 中的端点为 $v_i$ 。 ###### 输出格式 输出包含 $minDegree + 1$ 行，每行首先输出一个整数 $cnt_k$ ，表示 最小k-覆盖 的边集大小，紧接着输出 $cnt_k$ 个整数，表示属于 最小k-覆盖 的边的标号。边按输入顺序从 $1$ 开始标号。输出时不必按标号从小到大输出。 感谢@OrangeLee 提供的翻译

题目描述

You are given a bipartite graph $ G=(U,V,E) $ , $ U $ is the set of vertices of the first part, $ V $ is the set of vertices of the second part and $ E $ is the set of edges. There might be multiple edges. Let's call some subset of its edges 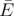 $ k $ -covering iff the graph 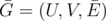 has each of its vertices incident to at least $ k $ edges. Minimal $ k $ -covering is such a $ k $ -covering that the size of the subset 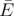 is minimal possible. Your task is to find minimal $ k $ -covering for each 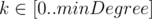, where $ minDegree $ is the minimal degree of any vertex in graph $ G $ .

输入输出格式

输入格式

The first line contains three integers $ n_{1} $ , $ n_{2} $ and $ m $ ( $ 1<=n_{1},n_{2}<=2000 $ , $ 0<=m<=2000 $ ) — the number of vertices in the first part, the number of vertices in the second part and the number of edges, respectively. The $ i $ -th of the next $ m $ lines contain two integers $ u_{i} $ and $ v_{i} $ ( $ 1<=u_{i}<=n_{1},1<=v_{i}<=n_{2} $ ) — the description of the $ i $ -th edge, $ u_{i} $ is the index of the vertex in the first part and $ v_{i} $ is the index of the vertex in the second part.

输出格式

For each 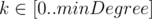 print the subset of edges (minimal $ k $ -covering) in separate line. The first integer $ cnt_{k} $ of the $ k $ -th line is the number of edges in minimal $ k $ -covering of the graph. Then $ cnt_{k} $ integers follow — original indices of the edges which belong to the minimal $ k $ -covering, these indices should be pairwise distinct. Edges are numbered $ 1 $ through $ m $ in order they are given in the input.

输入输出样例

输入样例 #1

3 3 7
1 2
2 3
1 3
3 2
3 3
2 1
2 1

输出样例 #1

0 
3 3 7 4 
6 1 3 6 7 4 5 

输入样例 #2

1 1 5
1 1
1 1
1 1
1 1
1 1

输出样例 #2

0 
1 5 
2 4 5 
3 3 4 5 
4 2 3 4 5 
5 1 2 3 4 5