Sonya and Matrix

题意翻译

题目描述 定义一种矩阵为“菱形矩阵”，它的大小为$n \times m$，且格子$(x_i,y_i)$中的权值为$|x_i-x|+|y_i-y|$，其中$x,y$是两个正整数，且有$1 \leq x \leq n , 1 \leq y \leq m$ 现给出$t$个非负整数，判断能否存在一个菱形矩阵矩阵元素由给出的$t$个非负整数构成。 输入 第一行一个正整数$t(1 \leq t \leq 10^6)$表示元素个数 接下来一行$t$个非负整数表示元素。 输出 如果存在，输出两行，第一行两个正整数$n,m(n \times m = t)$表示矩阵的长宽，第二行两个正整数$x,y(1 \leq x \leq n , 1 \leq y \leq m)$。 如果不存在，输出一行$-1$。

题目描述

Since Sonya has just learned the basics of matrices, she decided to play with them a little bit. Sonya imagined a new type of matrices that she called rhombic matrices. These matrices have exactly one zero, while all other cells have the Manhattan distance to the cell containing the zero. The cells with equal numbers have the form of a rhombus, that is why Sonya called this type so. The Manhattan distance between two cells ( $ x_1 $ , $ y_1 $ ) and ( $ x_2 $ , $ y_2 $ ) is defined as $ |x_1 - x_2| + |y_1 - y_2| $ . For example, the Manhattan distance between the cells $ (5, 2) $ and $ (7, 1) $ equals to $ |5-7|+|2-1|=3 $ . 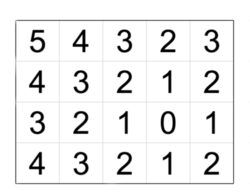Example of a rhombic matrix.Note that rhombic matrices are uniquely defined by $ n $ , $ m $ , and the coordinates of the cell containing the zero. She drew a $ n\times m $ rhombic matrix. She believes that you can not recreate the matrix if she gives you only the elements of this matrix in some arbitrary order (i.e., the sequence of $ n\cdot m $ numbers). Note that Sonya will not give you $ n $ and $ m $ , so only the sequence of numbers in this matrix will be at your disposal. Write a program that finds such an $ n\times m $ rhombic matrix whose elements are the same as the elements in the sequence in some order.

输入输出格式

输入格式

The first line contains a single integer $ t $ ( $ 1\leq t\leq 10^6 $ ) — the number of cells in the matrix. The second line contains $ t $ integers $ a_1, a_2, \ldots, a_t $ ( $ 0\leq a_i< t $ ) — the values in the cells in arbitrary order.

输出格式

In the first line, print two positive integers $ n $ and $ m $ ( $ n \times m = t $ ) — the size of the matrix. In the second line, print two integers $ x $ and $ y $ ( $ 1\leq x\leq n $ , $ 1\leq y\leq m $ ) — the row number and the column number where the cell with $ 0 $ is located. If there are multiple possible answers, print any of them. If there is no solution, print the single integer $ -1 $ .

输入输出样例

输入样例 #1

20
1 0 2 3 5 3 2 1 3 2 3 1 4 2 1 4 2 3 2 4

输出样例 #1

4 5
2 2

输入样例 #2

18
2 2 3 2 4 3 3 3 0 2 4 2 1 3 2 1 1 1

输出样例 #2

3 6
2 3

输入样例 #3

6
2 1 0 2 1 2

输出样例 #3

-1

说明

You can see the solution to the first example in the legend. You also can choose the cell $ (2, 2) $ for the cell where $ 0 $ is located. You also can choose a $ 5\times 4 $ matrix with zero at $ (4, 2) $ . In the second example, there is a $ 3\times 6 $ matrix, where the zero is located at $ (2, 3) $ there. In the third example, a solution does not exist.

题意翻译

题目描述 定义一种矩阵为“菱形矩阵”，它的大小为$n \times m$，且格子$(x_i,y_i)$中的权值为$|x_i-x|+|y_i-y|$，其中$x,y$是两个正整数，且有$1 \leq x \leq n , 1 \leq y \leq m$ 现给出$t$个非负整数，判断能否存在一个菱形矩阵矩阵元素由给出的$t$个非负整数构成。 输入 第一行一个正整数$t(1 \leq t \leq 10^6)$表示元素个数 接下来一行$t$个非负整数表示元素。 输出 如果存在，输出两行，第一行两个正整数$n,m(n \times m = t)$表示矩阵的长宽，第二行两个正整数$x,y(1 \leq x \leq n , 1 \leq y \leq m)$。 如果不存在，输出一行$-1$。