New Building for SIS

题意翻译

### 题目描述 你正在研究夏季信息学院新建筑的楼层设计。因为你担任着英国秘密情报局的后勤物流任务，所以你十分在乎去往不同位置的路程耗时：了解从演讲室到食堂，或者从健身房到服务器机房的耗时是很重要的。 这个建筑由 $n$ 个塔楼组成，标号为 $1 - n$ ；每个塔楼有 $h$ 层，标号为 $1 - h$ 。任意两个相邻的塔楼间有一条通道（当 $1 \le i \le n - 1$ 时，塔楼 $i$ 与 $i - 1$ 相连）。在第 $x ( a \le x \le b)$ 层上，你可以在与第 $x$ 层相邻的2层移动，或如果第 $x$ 层与相邻的塔楼有通道连通也可移动至其上。离开建筑是不被允许的。 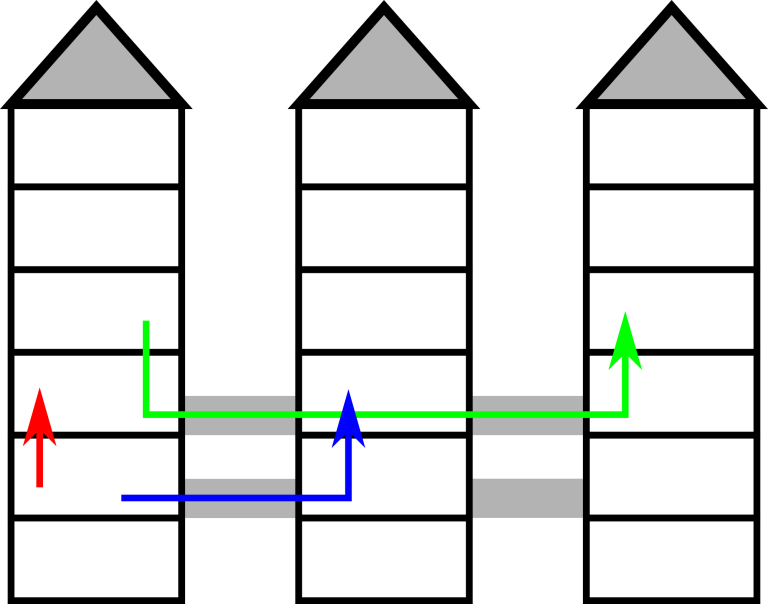 这个图片解释了 **输入 #1** 你将被给予 $k$ 对位置 $(t_a, f_a), (t_b, f_b)$ ：代表塔楼 $t_a$ 上的第 $f_a$ 层，塔楼 $t_b$ 上的第 $f_b$ 层。 对于每一对位置，你需要确定它们之间的最短耗时。 ### 输入格式 输入的第一行包含以下整数： - $n$ : 建筑中塔楼的个数 $(1 \le n \le 10^8)$ - $h$ : 塔楼的层数 $( 1 \le h \le 10^8)$ - $a$ 和 $b$ : 可以在相邻塔楼间移动的最低与最高楼层限制 $(1 \le a \le b \le h)$ - $k$ : 给予的位置个数 $ (1 \le k \le 10^4) $ 接下来 $k$ 行，是每对位置的详细数据，每对数据包括四个整数 $t_a, f_a, t_b, f_b (1 \le t_a, t_b \le n, 1 \le f_a, f_b \le h)$ 你需要确定它们间的最短耗时。 ### 输出格式 对于每对位置，回应一个整数，为两地之间最短路程耗时。

题目描述

You are looking at the floor plan of the Summer Informatics School's new building. You were tasked with SIS logistics, so you really care about travel time between different locations: it is important to know how long it would take to get from the lecture room to the canteen, or from the gym to the server room. The building consists of $ n $ towers, $ h $ floors each, where the towers are labeled from $ 1 $ to $ n $ , the floors are labeled from $ 1 $ to $ h $ . There is a passage between any two adjacent towers (two towers $ i $ and $ i+1 $ for all $ i $ : $ 1<=i<=n-1 $ ) on every floor $ x $ , where $ a<=x<=b $ . It takes exactly one minute to walk between any two adjacent floors of a tower, as well as between any two adjacent towers, provided that there is a passage on that floor. It is not permitted to leave the building. The picture illustrates the first example. You have given $ k $ pairs of locations $ (t_{a},f_{a}) $ , $ (t_{b},f_{b}) $ : floor $ f_{a} $ of tower $ t_{a} $ and floor $ f_{b} $ of tower $ t_{b} $ . For each pair you need to determine the minimum walking time between these locations.

输入输出格式

输入格式

The first line of the input contains following integers: - $ n $ : the number of towers in the building ( $ 1<=n<=10^{8} $ ), - $ h $ : the number of floors in each tower ( $ 1<=h<=10^{8} $ ), - $ a $ and $ b $ : the lowest and highest floor where it's possible to move between adjacent towers ( $ 1<=a<=b<=h $ ), - $ k $ : total number of queries ( $ 1<=k<=10^{4} $ ). Next $ k $ lines contain description of the queries. Each description consists of four integers $ t_{a} $ , $ f_{a} $ , $ t_{b} $ , $ f_{b} $ ( $ 1<=t_{a},t_{b}<=n $ , $ 1<=f_{a},f_{b}<=h $ ). This corresponds to a query to find the minimum travel time between $ f_{a} $ -th floor of the $ t_{a} $ -th tower and $ f_{b} $ -th floor of the $ t_{b} $ -th tower.

输出格式

For each query print a single integer: the minimum walking time between the locations in minutes.

输入输出样例

输入样例 #1

3 6 2 3 3
1 2 1 3
1 4 3 4
1 2 2 3

输出样例 #1

1
4
2