Lost Root

题意翻译

本题为交互题 题意：有一棵节点编号未知的满$k$叉树，其上有$n$个节点，你每次可以询问一个点是否在另两个点的路径上。需要在$60*n$次询问操作中找到这棵树的根。 输入：第一行两个正整数$n$和$k$($3\le n \le1500$,$2 \le k \le n$) 询问操作的格式为$"?\ a\ b\ c"$代表询问$b$是否在$a$到$c$的路径上 每个询问后你需要读入$Yes$或$No$,代表询问的答案。 输出根时格式为$"!\ s"$ 代表你的答案为$s$。 询问超过限定次数(~~好像会?~~)返回WA

题目描述

The graph is called tree if it is connected and has no cycles. Suppose the tree is rooted at some vertex. Then tree is called to be perfect $ k $ -ary tree if each vertex is either a leaf (has no children) or has exactly $ k $ children. Also, in perfect $ k $ -ary tree all leafs must have same depth. For example, the picture below illustrates perfect binary tree with $ 15 $ vertices: 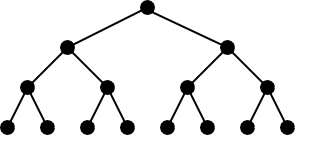There is a perfect $ k $ -ary tree with $ n $ nodes. The nodes are labeled with distinct integers from $ 1 $ to $ n $ , however you don't know how nodes are labelled. Still, you want to find the label of the root of the tree. You are allowed to make at most $ 60 \cdot n $ queries of the following type: - "? $ a $ $ b $ $ c $ ", the query returns "Yes" if node with label $ b $ lies on the path from $ a $ to $ c $ and "No" otherwise. Both $ a $ and $ c $ are considered to be lying on the path from $ a $ to $ c $ . When you are ready to report the root of the tree, print - "! $ s $ ", where $ s $ is the label of the root of the tree. It is possible to report the root only once and this query is not counted towards limit of $ 60 \cdot n $ queries.

输入输出格式

输入格式

输出格式

The first line of the standard input stream contains two integers $ n $ and $ k $ ( $ 3 \le n \le 1500 $ , $ 2 \le k < n $ ) — the number of nodes in the tree and the value of $ k $ . It is guaranteed that $ n $ is such that the tree forms a perfect $ k $ -ary tree. You can ask at most $ 60 \cdot n $ queries. To ask a query, print a line of form "? $ a $ $ b $ $ c $ ", where $ 1 \le a, b, c \le n $ . After that you should read a single line containing "Yes" or "No" depending on the answer of the query. The tree is fixed for each test and it doesn't depend on your queries. When you are ready to print the answer, print a line of the form "! $ s $ ", where $ s $ is the label of the root vertex and then terminate your program. After printing each query do not forget to print end of line and flush the output. Otherwise you may get Idleness limit exceeded. To do this, use: - fflush(stdout) or cout.flush() in C++; - System.out.flush() in Java; - flush(output) in Pascal; - stdout.flush() in Python; - See documentation for other languages. In case your program will make more than $ 60 \cdot n $ queries, but in other aspects would follow the interaction protocol and terminate coorectly, it will get verdict «Wrong Answer». Hacks To hack the solution use the following test format: The first line should contain integers $ n $ and $ k $ ( $ 3 \le n \le 1500 $ , $ 2 \le k \le 1500 $ ) — the number of vertices and the $ k $ parameter of the tree. Of course, the value of $ n $ must correspond to the size of the valid $ k $ -ary tree of some depth. The second line should contain $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le n $ ) — the labels of the tree in the natural order, all labels must be distinct. Let's call the following ordering of the tree vertices to be natural: first the root of the tree goes, then go all vertices on depth of one edge from root, ordered from left to right, then go all vertices on depth of two edges from root, ordered from left to right, and so on until the maximum depth. This way, the $ a_1 $ is the answer for the hack.

输入输出样例

输入样例 #1

3 2

No

Yes

输出样例 #1

? 1 3 2

? 1 2 3

! 2

说明

The tree in the example is as follows: The input and output for example illustrate possible interaction on that test (empty lines are inserted only for clarity). The hack corresponding to the example would look like: `<br></br>3 2<br></br>2 3 1<br></br>`