305911: CF1109C. Sasha and a Patient Friend
Memory Limit:256 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Sasha and a Patient Friend
题意翻译
费迪亚和萨沙是朋友,所以萨沙项知道关于费迪亚的一切。 费迪亚把他的耐心放在一个无限大的碗里。(真实么) 但是,与碗不同,费迪亚的耐心不是无限的,费迪亚总共有$v$升的耐心,一旦$v$等于$0$,碗将立即破裂。 碗里有一个水龙头,可以每秒增加$s$升的耐心。请注意,$s$可能是负数,在这种情况下,水龙头会吸入耐心(……) 萨沙可以做不同的事情,所以他可以改变水龙头的速度。萨沙所做的所有动作都可以表示为$q$次操作。有三种类型的操作: ```1 t s```-添加一个新速度,意味着从第$t$秒开始,水龙头的速度将等于$s$。 ```2 t```-删除第$t$秒发生的操作。保证此类操作的存在。 ```3 l r v```-萨沙想知道:如果按照所有$l \le t\le r$的操作来执行,那么碗何时会破裂。如果碗在规定时间内没发生破裂,那么答案将是$-1$. 由于萨沙不想检查费迪亚的耐心结束后会发生什么,所以他请求你帮助他,并回答每一个第$3$类问题。 保证在任何时刻,不会有两个事件同时发生。 ### 输入格式 第一行包含一个整数$q$($1\le q\le 10^5 $),表示查询的数量。 接下来的每一行$q$都有以下格式之一: ```1 t s```$(1\le t\le 10^9,-10^9\le s\le 10^9)$,含义如题。 ```2 t```$(1\le t\le 10^9)$,含义如题。 ```3 l r v```$(1\le l\le r\le 10^9,0\le v\le 10^9$),含义如题。 保证所有查询中的$t$、$s$、$l$、$r$、$v$都是整数。 另外,保证至少有一个$3$类型的查询。 ### 输出格式 对于第$3$种类型的每个查询,输出一个整数,表示结果。 如果绝对或相对误差不超过$10^{-6}$,您的答案将被视为正确。 也就是说,你的答案是$a$,测试点的答案是$b$。当且仅当$\frac{∣a−b∣}{max(1,∣b∣)} \le 10 ^{−6}$ 时你才会拿到该测试点的分。 ### 样例解释 在第一个样例中,$3$类型的所有查询都包含所有事件,其模拟如下: 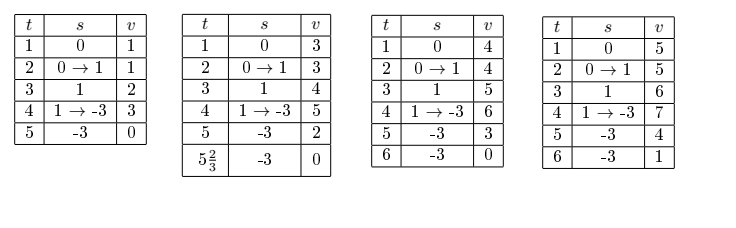 Translated by 桂梓清 2022.1.4题目描述
Fedya and Sasha are friends, that's why Sasha knows everything about Fedya. Fedya keeps his patience in an infinitely large bowl. But, unlike the bowl, Fedya's patience isn't infinite, that is why let $ v $ be the number of liters of Fedya's patience, and, as soon as $ v $ becomes equal to $ 0 $ , the bowl will burst immediately. There is one tap in the bowl which pumps $ s $ liters of patience per second. Notice that $ s $ can be negative, in that case, the tap pumps out the patience. Sasha can do different things, so he is able to change the tap's speed. All actions that Sasha does can be represented as $ q $ queries. There are three types of queries: 1. "1 t s" — add a new event, means that starting from the $ t $ -th second the tap's speed will be equal to $ s $ . 2. "2 t" — delete the event which happens at the $ t $ -th second. It is guaranteed that such event exists. 3. "3 l r v" — Sasha wonders: if you take all the events for which $ l \le t \le r $ and simulate changes of Fedya's patience from the very beginning of the $ l $ -th second till the very beginning of the $ r $ -th second inclusive (the initial volume of patience, at the beginning of the $ l $ -th second, equals to $ v $ liters) then when will be the moment when the bowl will burst. If that does not happen, then the answer will be $ -1 $ . Since Sasha does not want to check what will happen when Fedya's patience ends, and he has already come up with the queries, he is asking you to help him and find the answer for each query of the $ 3 $ -rd type. It is guaranteed that at any moment of time, there won't be two events which happen at the same second.输入输出格式
输入格式
The first line contans one integer $ q $ ( $ 1 \le q \le 10^5 $ ) — the number of queries. Each of the next $ q $ lines have one of the following formats: - 1 t s ( $ 1 \le t \le 10^9 $ , $ -10^9 \le s \le 10^9 $ ), means that a new event is added, which means that starting from the $ t $ -th second the tap's speed will be equal to $ s $ . - 2 t ( $ 1 \le t \le 10^9 $ ), means that the event which happens at the $ t $ -th second must be deleted. Guaranteed that such exists. - 3 l r v ( $ 1 \le l \le r \le 10^9 $ , $ 0 \le v \le 10^9 $ ), means that you should simulate the process from the very beginning of the $ l $ -th second till the very beginning of the $ r $ -th second inclusive, and to say when will the bowl burst. It is guaranteed that $ t $ , $ s $ , $ l $ , $ r $ , $ v $ in all the queries are integers. Also, it is guaranteed that there is at least one query of the $ 3 $ -rd type, and there won't be a query of the $ 1 $ -st type with such $ t $ , that there already exists an event which happens at that second $ t $ .
输出格式
For each query of the $ 3 $ -rd type, print in a new line the moment when the bowl will burst or print $ -1 $ if it won't happen. Your answer will be considered correct if it's absolute or relative error does not exceed $ 10^{-6} $ . Formally, let your answer be $ a $ , and the jury's answer be $ b $ . Your answer is accepted if and only if $ \frac{|a - b|}{\max{(1, |b|)}} \le 10^{-6} $ .
输入输出样例
输入样例 #1
6
1 2 1
1 4 -3
3 1 6 1
3 1 6 3
3 1 6 4
3 1 6 5
输出样例 #1
5
5.666667
6
-1
输入样例 #2
10
1 2 2
1 4 4
1 7 -10
3 2 4 1
3 5 6 0
3 1 15 1
2 4
3 1 15 1
1 8 1
3 1 15 1
输出样例 #2
-1
5
8.7
8.1
-1
输入样例 #3
5
1 1000 9999999
1 2000 -9999
3 1000 2000 0
2 1000
3 1000 2002 1
输出样例 #3
1000
2000.0001